Introduction

人工智慧/機器學習是啥

人工智慧：希望機器跟人一樣聰明

機器學習：機器具有學習的能力

深度學習：機器學習的一種方法

人工智慧是我們的目標，機器學習是達成目標的手段

機器學習的本質

機器學習的本質就是為輸入資料找出相應的函數

像是 f(貓的圖片) = “貓”

架構如下：

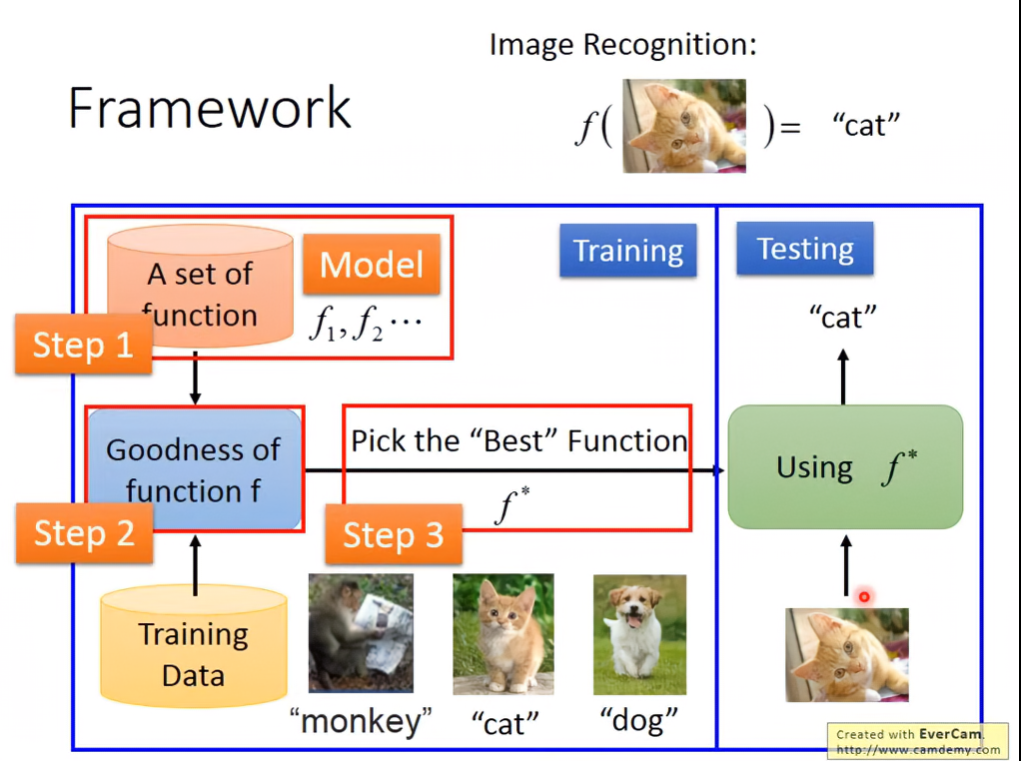
在某個function set透過訓練資料，找出最好的function，並測試這個function的可靠性。

Learning map

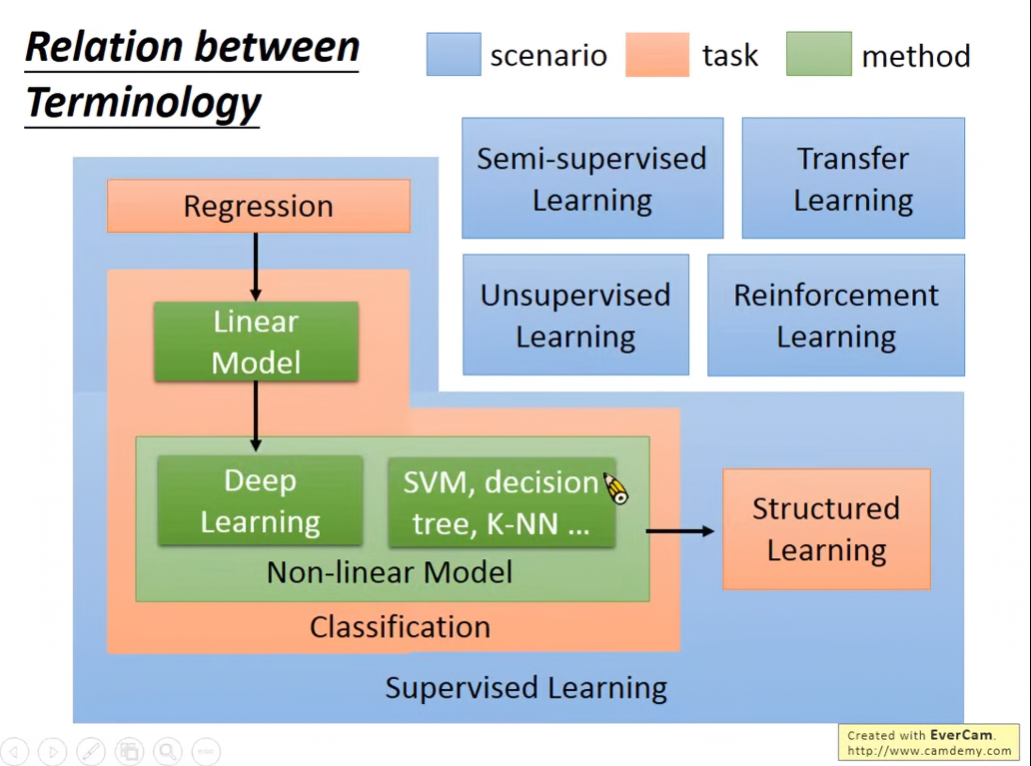
Regression：透過過往資料，預測未來訊息，不管輸入資料類型為什麼，輸出總是純量。

Classification：

• Binary Classification：判斷輸入資料，輸出僅有是或否

• Multi-class Classification：將資料分類成多個類別

Supervised Learning：給機器提供輸入資料與預期輸出，讓機器找出function

Semi-Supervised Learning：給機器少量有label的資料，與大量沒label的資料

Transfer Learning：給機器少量有label的資料，與大量不相關的資料(可能有label也可能沒有)

Unsupervised Learning：給機器完全沒有label的資料

Structured Learning：讓機器輸出有結構性的資料

Reinforcement Learning：不告訴機器正確答案，機器只會知道自己做的好還是不好，做的不好就回去改進。跟監督式學習的差別在於，監督式很像learning from teacher，而Reinforcement是learning from criticis。

Lecture 1: Regression

Regression Problem

從過去的資料預測未來。例如從過去十年各種股票起伏的資料，預測未來的道瓊指數。從無人車的各個sensor資料，推測要控制的方向盤角度。

Procedure

Step 1: Model

確定輸入資料想要的輸出資料 ⇒ 找出各種function，形成function set

如果function被定義為線性函數，則此model被稱為linear model

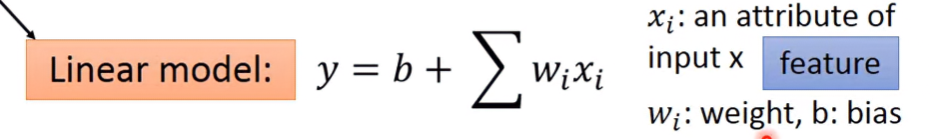
Step 2: Goodness of Function

收集足夠多的training data，並測試每個function的好壞。

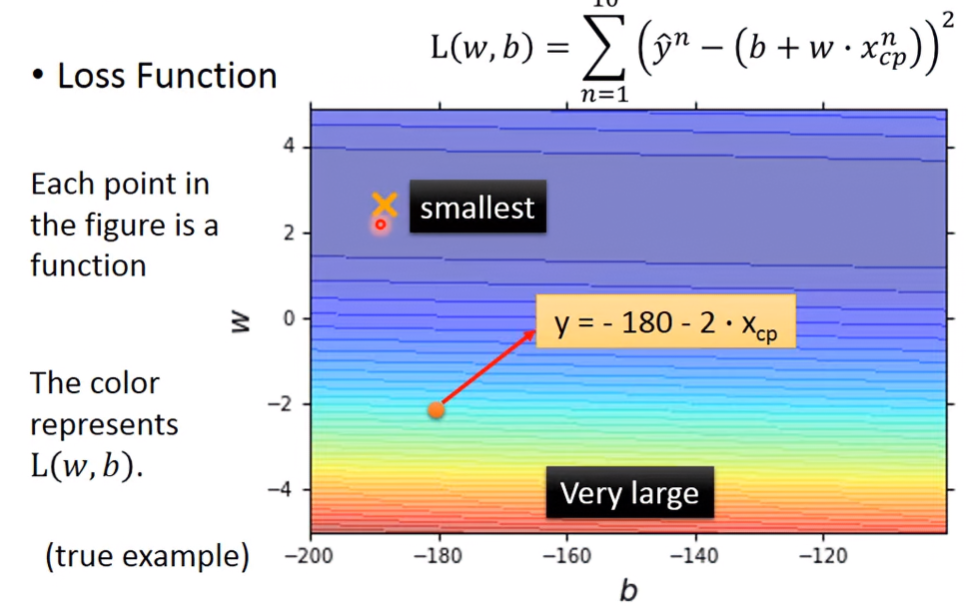
Loss function (L):

• Input: a function

• Output: how bad it is

Loss function example: 真正數值減預估數值後取平方的加總

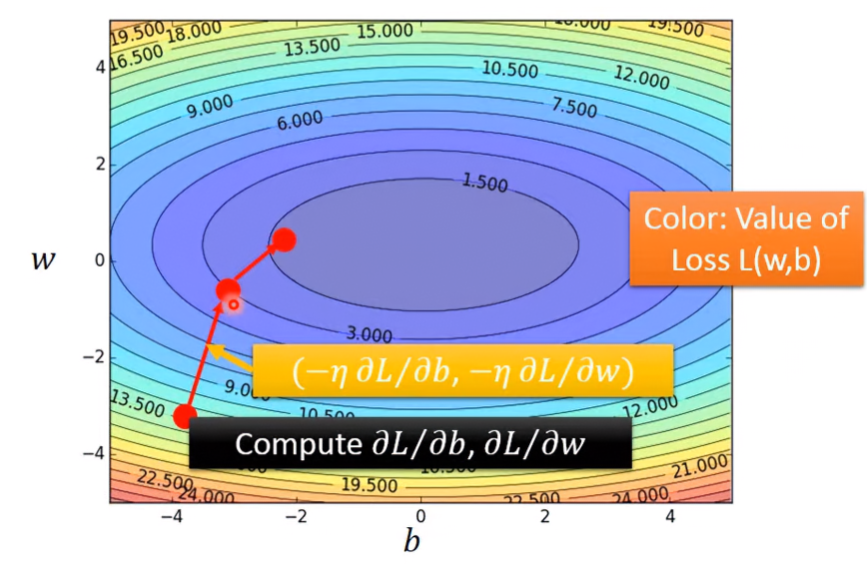
圖形化loss function，越紅色loss越大，誤差越大；越藍色loss越小，誤差越小。

Step 3: Best Function

從function set裡找出最佳的function f*，而f*就是loss最小的function。找一個f使得L(f)最小：

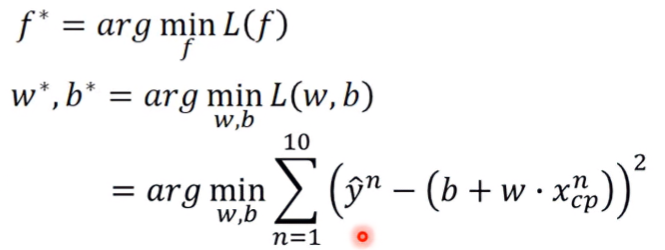
可以窮舉w和b，找出最好的結果。這個函數有closed-form solution(把所有參數組合代入，可找出最佳解)

但這樣太不實際了，所以就使用Gradient descent，找出較好解

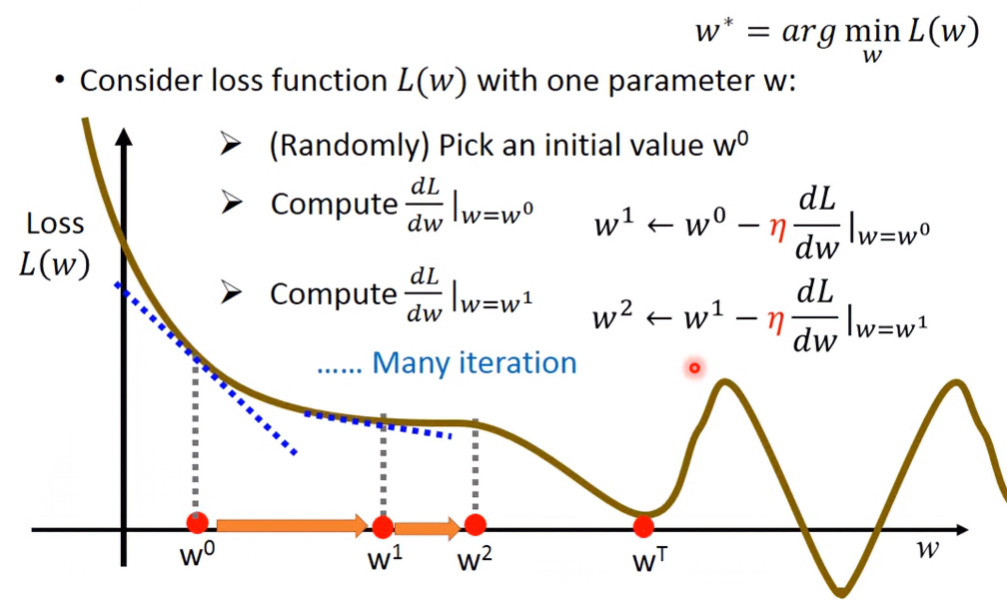
Gradient Descent：

• 隨機選取w0。計算w=w0時，L對w的導數。
  • 若導數為負，代表在w0附近靠右區間內為單調向下函數，要增加w的值
  • 若導數為正，代表在w0附近靠左區間內為單調向上函數，要減少w的值

• 令w1 = w0 - η*dL/dw，重複迭代，直到找到minimum。(η: learning rate)

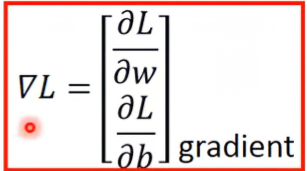
多變數Grdient Descent(以兩變數w, b為例)：

• 求L在w=0、b=0時，對w及b的偏導數

• 令w1 = w0 - η*∂L/∂w，b1 = b0 - η*∂L/∂b，重複迭代直到找到minimum

簡單來說就是求Gradient

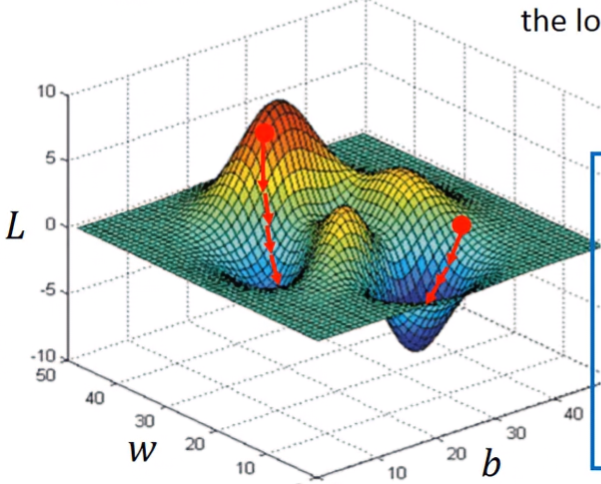
local minimum問題

因為這是linear regression，是convex function，不會有local minimum的問題，所以就如左圖，不管一開始w0、b0值取多少，最後都會落到最低點；而右圖就是non-linear regression，若w0、b0值取錯，就會落入local minimum，導致無法求得最佳解

Solution of gradient of w and b

Model Selection

Traning Data

選用的model越複雜，training data的loss會越小，這是因為function space包含的元素隨複雜度增加

Training Data v.s. Testing Data

雖然代入Training Data時，model越複雜loss越小。但代入Testing Data的結果就不一樣了，model複雜度越高，反而loss越大。這個現象被稱作overfitting。就很像在駕訓班練習開車時還開得不錯，但上路後就又不好說了。所以應該要選最適合的model，而不是最複雜的model。

Redesign the Model

因為這麼多的資料，可能會有好幾個不同種類，所以如果沒分類就使用同個model，就不會找到最佳解。所以不同種類的資料，就要有不同linear function：

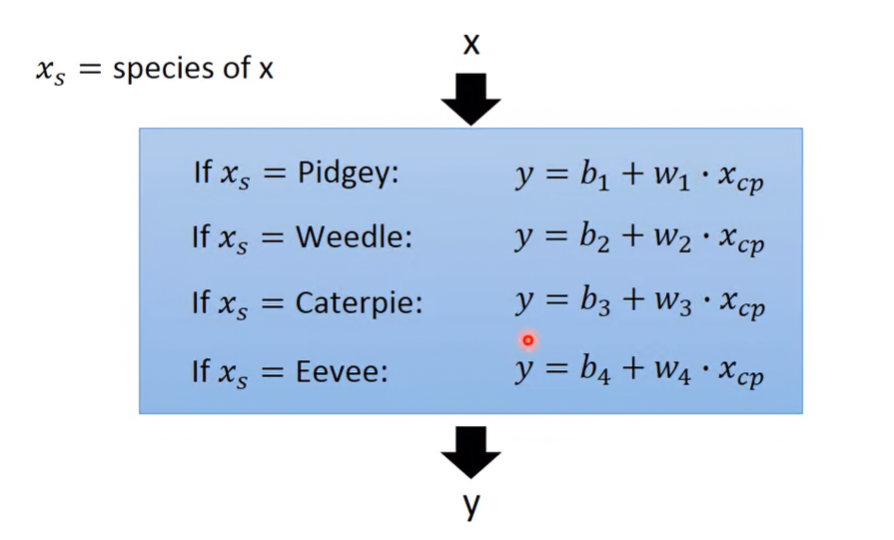
單有這麼多組的function，這樣model還是線性的嗎？所以我們可以把y用delta function的組合表示：

Regularization

隨著model的複雜度與考慮的參數量增加，但loss不會跟著下降，反而上升，有overfitting
發生。所以我們現在要重新設計loss function：

λ為常數項，我們原本的loss function，再考慮了權重的加總。為甚麼呢？

先考慮下y，當輸入x有變化時，則輸出y的變化受w影響，也就是x被w的放大或縮小：

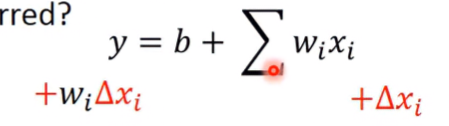
所以如果loss function加入了權重項的考慮，則當我們希望loss變小時，變相希望w變小。當w變小，則輸入x的變化量越不明顯，函數會變得更平滑(smooth)。換句話說就是當x有雜訊時，雜訊對輸出的影響會變小，使得loss function更能找出最佳解。

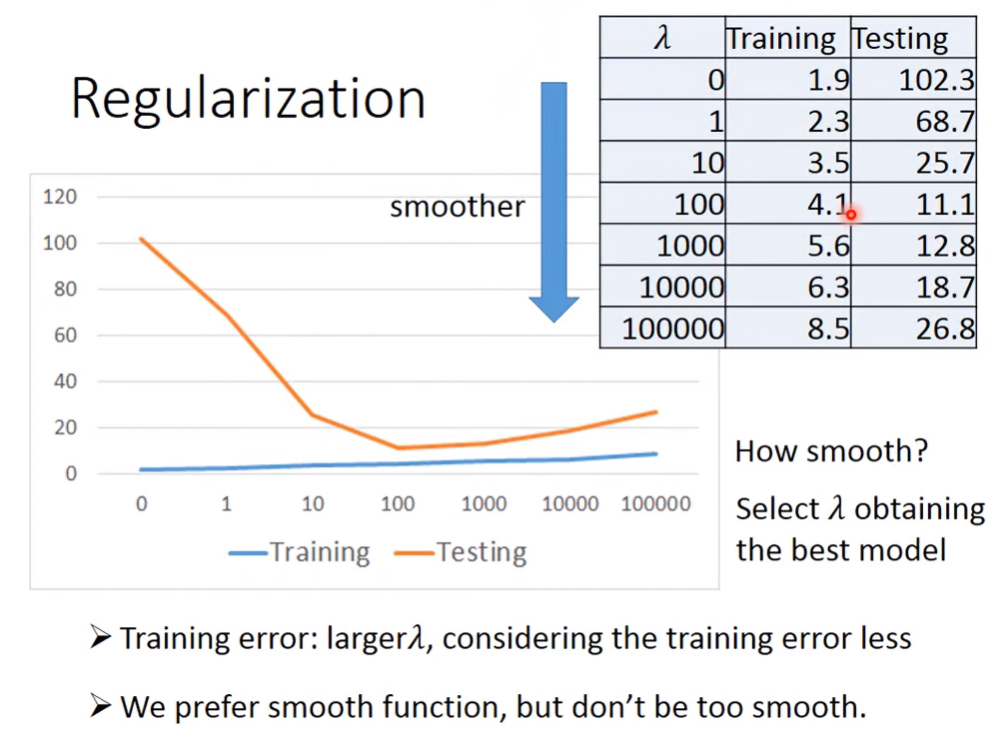
λ控制了平滑程度，當λ越大，則函數越平滑，testing data得到的結果更精確。不過當λ超過一個閥值，則loss反而會上升，所以λ不是越大越好。

那b為甚麼不用考慮？因為b(bias)是控制函數上下的平移，對於函數的平滑性無關係。

Lecture 2: Where does the error come from ?

模型越複雜不代表模型越準確，導致這現象的錯誤分為兩種：bias、variance

假設我們要預測的事件，其真實函數為f_hat，我們預測的模型為f*。在真實情況中，若以打靶形容，f_hat就是中心紅點，我們預測的f*實際上不會正中紅心，而f*到f_hat的差距，就是bias與variance的總和：

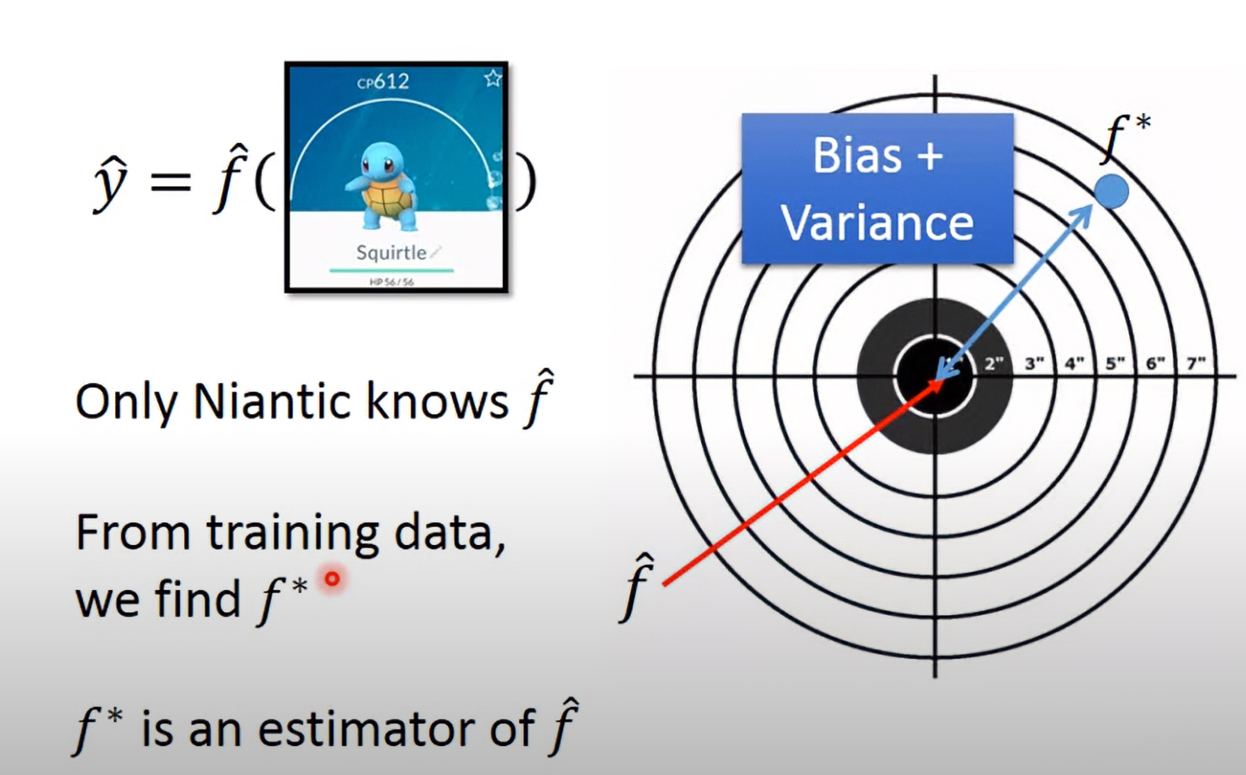
Bias and Variance of Estimator

因為無法知道整體資料的全貌，所以只好從中取樣N筆資料來估計特徵。假設取樣了N筆資料: {x_1, x_2, …, X_N}，則樣本平均值m為全部資料的加總除以N，期望值E[m]如下：

m為某次取樣的估計量(Estimator)，當重複進行非常多次隨機取樣，則每次取樣的m的平均值(期望值)E[m]會非常接近真實值 μ。

多次取樣的結果的之間的差異值Var[m]為變異數(variance)σ²除以N，σ²代表每筆資料的變動程度，表示資料本身的穩定性。

(直線圖上的文字有錯，左邊應為Smaller N，右邊應為Larger N)
圖上的每顆藍點代表在進行多次取樣時，每一次取樣的m，當取樣數越大，則每個取樣的預估值m之間的差異就越小，也越靠近真實數。下圖為無偏時的樣本離散程度。

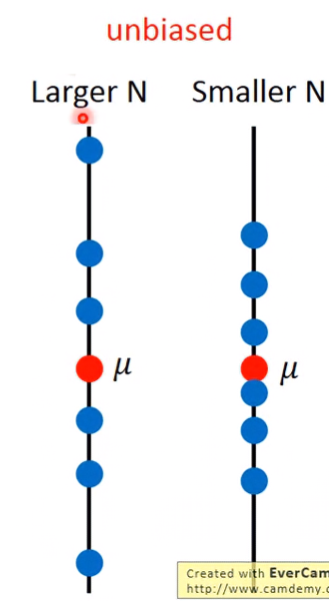
Unbiased就很像在打靶時一開始有瞄準紅心，但因為風力等影響，導致每次射到的都會有偏差，但整體平均來說會接近紅心；Biased就很像一開始就射歪，導致整體平均後，離原本的紅心還有偏差，所以期望值需乘上N-1/N來校正：

以打靶來比喻，就會像下面這樣：

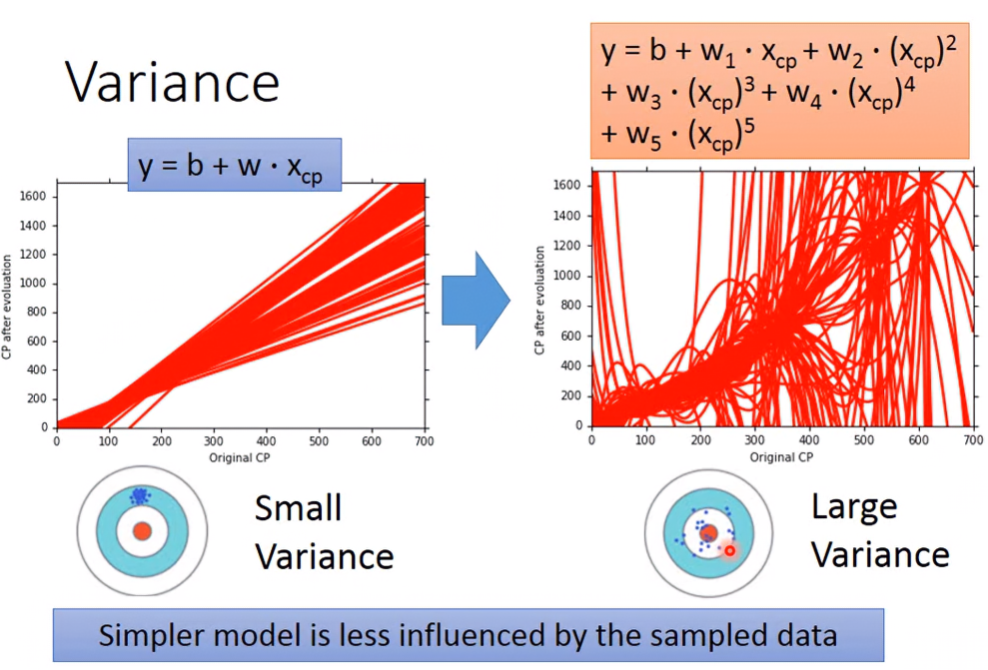
Variance

假設我們有100筆資料，每次取樣10筆。可以看到模型越簡單，其圖形較集中，則Variance小；模型越複雜，其圖形散布程度越大，variance大。

簡單的model受到不同data的影響比較小，所以每個模型的差別就不會那麼大；複雜的model反之。

Bias

f*為每次訓練的結果，f_bar為所有訓練結果的平均，可以想像f_bar為中心點，每個f*都以f_bar為中心點散開。

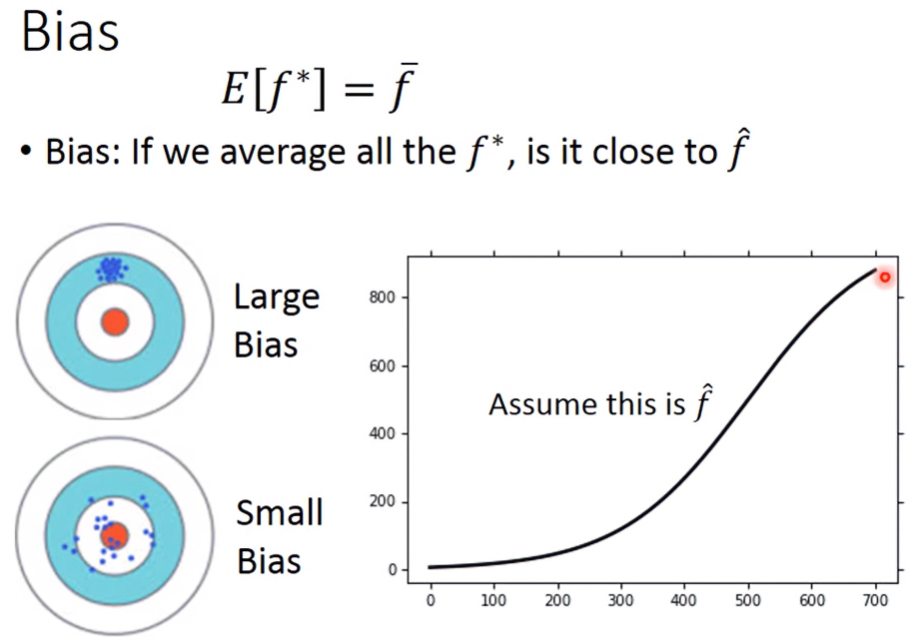
當模型簡單，就好像在取樣時的function space比較不會有機會包含target，導致bias變大；模型複雜，則function space包含target的機率就變大，bias較小。

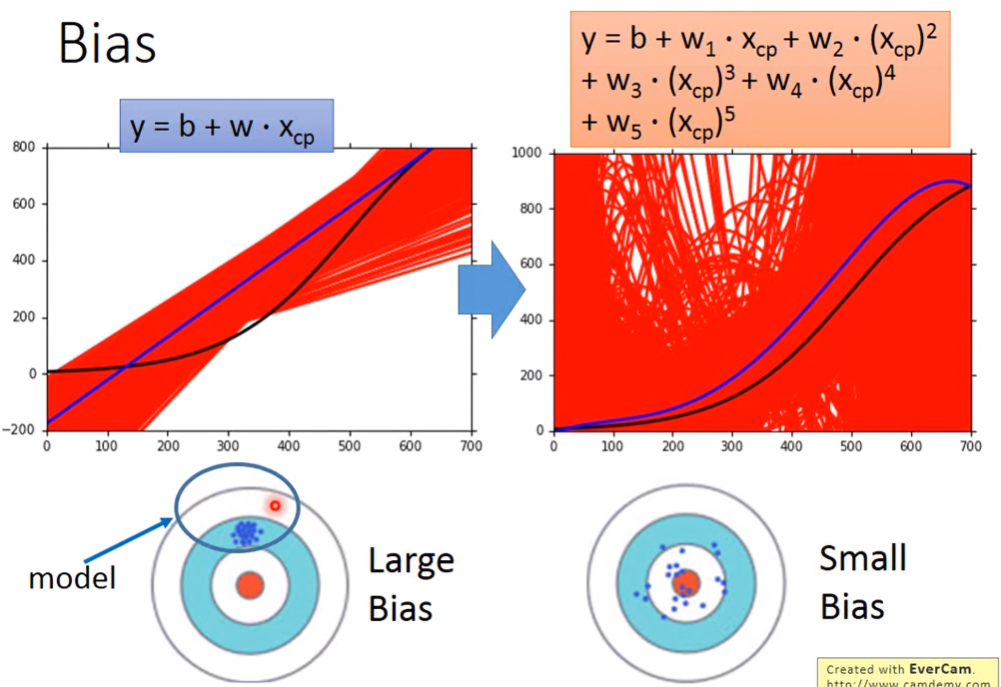
Bias v.s. Variance

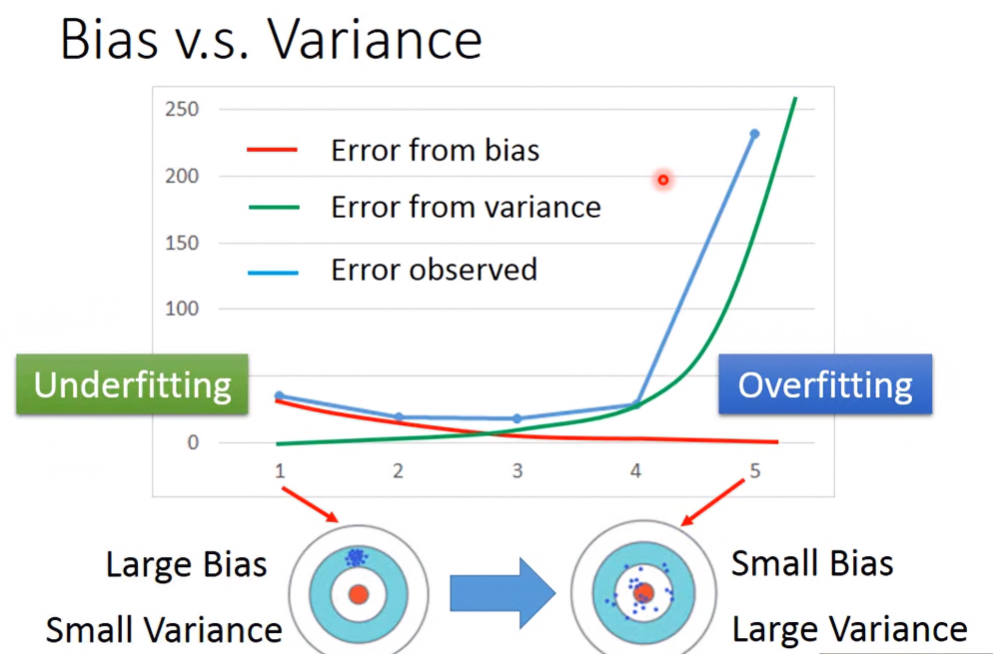
當模型簡單、bias大、variance小時，稱作underfitting，此時要把更多的feature考慮進model，或把model變得更複雜；當模型複雜、bias小、variance大時，稱作overfitting。

解決overfitting的方法：

• 收集更多資料：此法最佳，且不會動到bias，但不實際。不過可以自己製造假的但合理的training data，像是：
  • 做數字影像辨識，可以把數字左轉15度、右轉15度，這樣原本只有一個data，就可以變成3個。
  • 希望能辨識公車上的語音，但我們只有錄音室乾淨的語音。可以去公車上路雜音，再加進錄音室錄的語音裡。

• Regularization：調整model的weight，使曲線變平滑、集中。但因為這樣會改變function space，所以有可能會動到bias。

Model Selection

• 在bias跟variance之間權衡，使總error最小

要注意的事情

如下圖，將自己手上的testing set丟入各model後，發現model 3的error是最小的，但其實把真實的testing set拿去測試，會發現實際上model 3的error不一定是最小的。

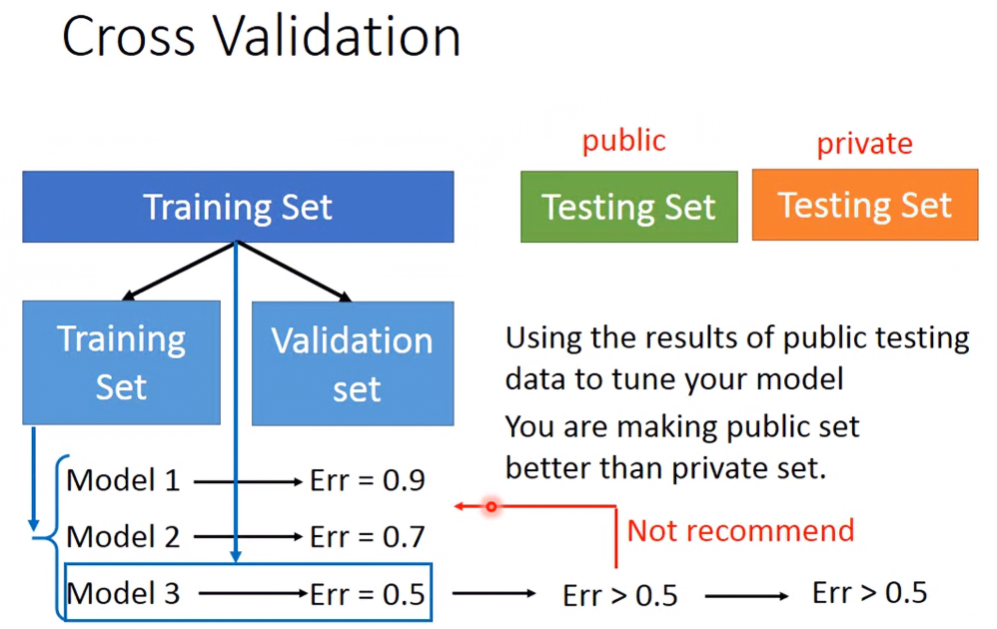
Cross Validation

將原本的Training Set分為Training Set跟Validation Set，Validation Set用來測驗model後選擇error最小的，此時選出的model以Public Training Set測出來的Error跟Private Testing Set測出來的Error不會差太多。

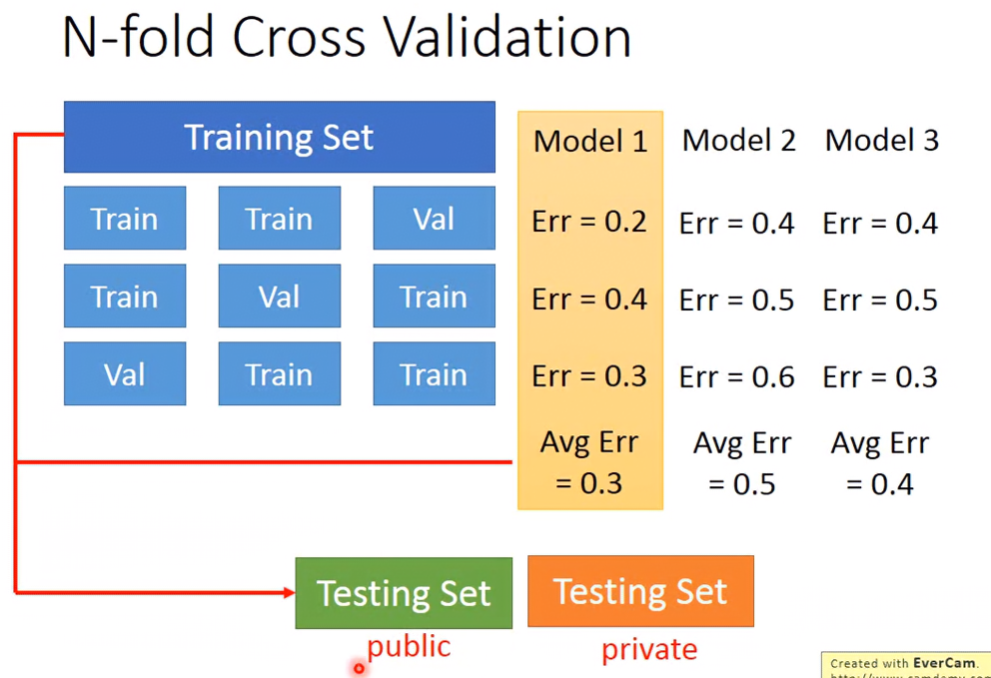
N-fold Cross Validation

Cross Validation的Validation Set的bias也有可能發生劣質的現象，此時若使用N-fold Cross Validation可能會更好。

以3-fold Cross Validation為例：

• 將Traing Set分為三組，每組各有兩個Training Set、一個Validation Set，每組的Training Set跟Validation Set皆不同。

• 訓練三個model，且每個模型都測試這三組的Validation Set，將每組測出來的error取平均，並選平均error最小的。

• 以整個Training Set去訓練選出的model。

• 最後把model丟到Public/Private Testing Set

不要太在意Public Testing Set的結果

如果覺得Public Testing Set的結果比Validation Set的結果還差，然後去調整原本的model的話，會導致原本model受Public Testing Set的Bias的汙染，結果Private Testing Set的結果可能還會變得更差。