Lecture 3~4

Lecture 3: Gradient Descent

Review

我們的目標是要找怎樣的參數能讓loss最小

\theta^* = \arg\min_{\theta} L(\theta)

假設loss function有兩參數，則一開始隨機選取的參數值為

\theta^0 = \begin{bmatrix} \theta_1^0 \\ \theta_2^0 \end{bmatrix}

上標為迭代次數，下標區分不同參數。

因此，gradient descent的迭代可表達為

\begin{bmatrix}\theta_1^1 \\\theta_2^1\end{bmatrix}=\begin{bmatrix}\theta_1^0 \\\theta_2^0\end{bmatrix}- \eta\begin{bmatrix}\frac{\partial L(\theta_1^0)}{\partial \theta_1} \\\frac{\partial L(\theta_2^0)}{\partial \theta_2}\end{bmatrix}

因為梯度的定義為

\nabla L(\theta) =\begin{bmatrix}\frac{\partial C(\theta_1)}{\partial \theta_1} \\\frac{\partial C(\theta_2)}{\partial \theta_2}\end{bmatrix}

因此，grandient descent可表達為

\theta^1 = \theta^0 - \eta \nabla L(\theta^0)

注意！ $\theta^1, \theta^0, \nabla L(\theta^0)$ 皆為向量！

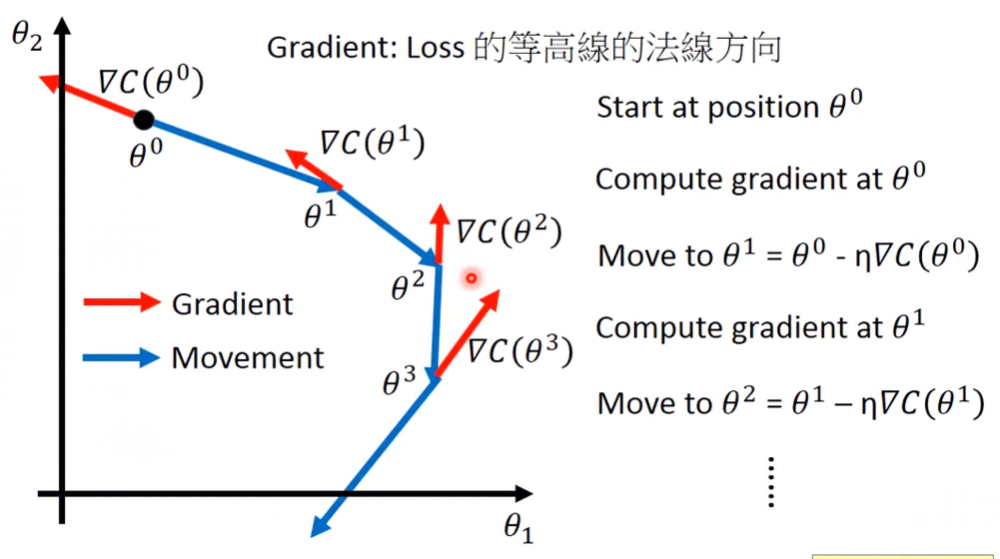
Gradient Descent視覺化來看會長這樣

Learning Rate

learning rate調太小會跑得很慢；調太高又有可能一直無法到達最低點

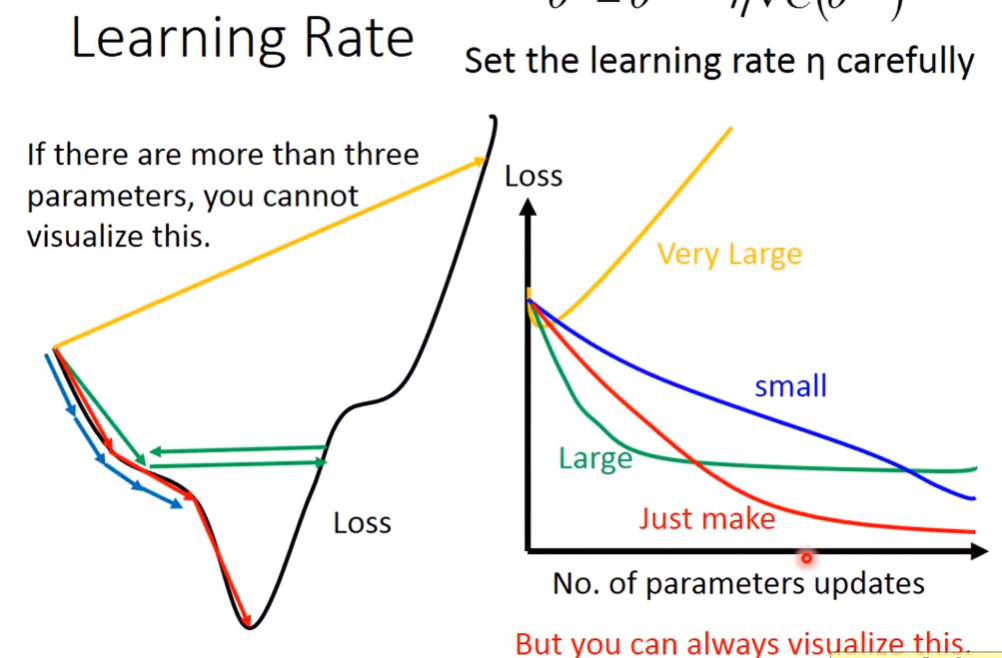
於是我們可以動態調整learning rate，稱為Adaptive Learning Rate。

Adaptive Learning Rate

在一開始，為了使學習更快點，所以將learning rate調大；隨著學習次數變多，為了更準確找到低點，因此將learning rate調小。以數學式表達：

\eta^t=\frac{\eta}{\sqrt{t+1}}

但這樣還是不夠，最好是不同的參數給不同的learning rate。

Method of Find great learning rate: dagrad

每一個參數的learing rate都除以之前導數的平均平方根(root mean square of its previous derivatives)。因此，gradient descent的數學式可表達為：

w^{t+1}=w^t-\frac{\eta^t}{\sigma^t}g^t

$\sigma^t$ : root mean square of the previous derivatives of parameter w

以數學式表達 $\sigma^t$ ：

\sigma^t = \sqrt{ \frac{1}{t+1} \sum_{i=0}^{t} (g^i)^2 }

合併至 $w^{t+1}$ ：

w^{t+1}=w^t-\frac{\eta}{\sqrt{\sum_{i=0}^{t}(g^i)^2}}g^t

從此公式可以看到有矛盾點：微分值越大，則分母也跟著變大；微分值越小，則分母變化沒多大。這點不是那麼直觀，以下詳細解釋。

Adagrad - explanation of formula

單變數函數

觀察某二次函數 $ax^2+bx+c$ ，其透過公式解可求出最低點位於 $-\frac{b}{2a}$ ，則對於函數上某點 $x_0$ ，其到最低點的距離為 $|x_0+\frac{b}{2a}|=\frac{|2ax_0+b|}{2a}$ ，可以發現分子是函數的一次微分函數 $|\frac{\partial y}{\partial x}|=|2ax+b|$

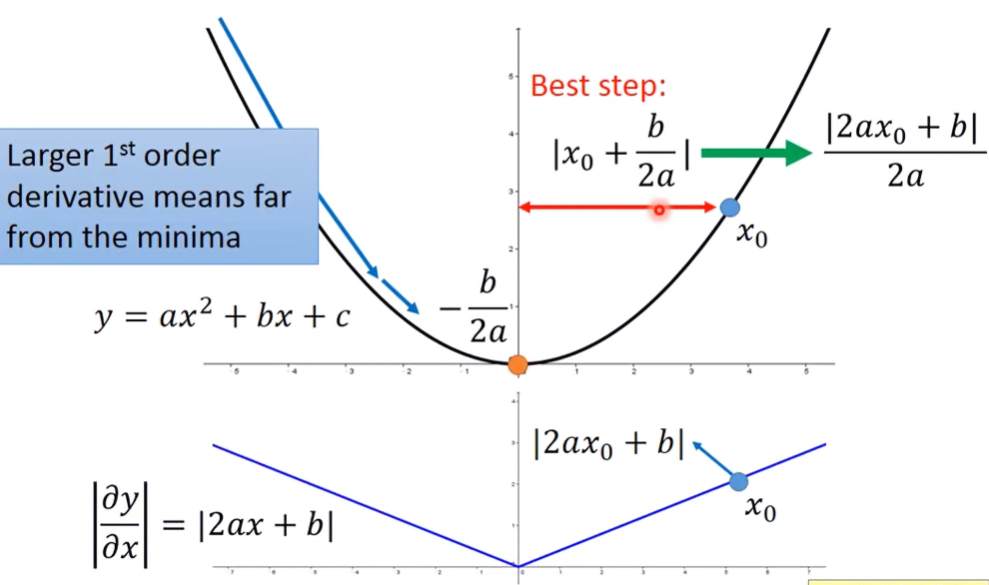
那分母的2a呢？2a又起到什麼作用？我們先來看多變數函數。

多變數函數－以雙變數 $w_1,w_2$ 為例

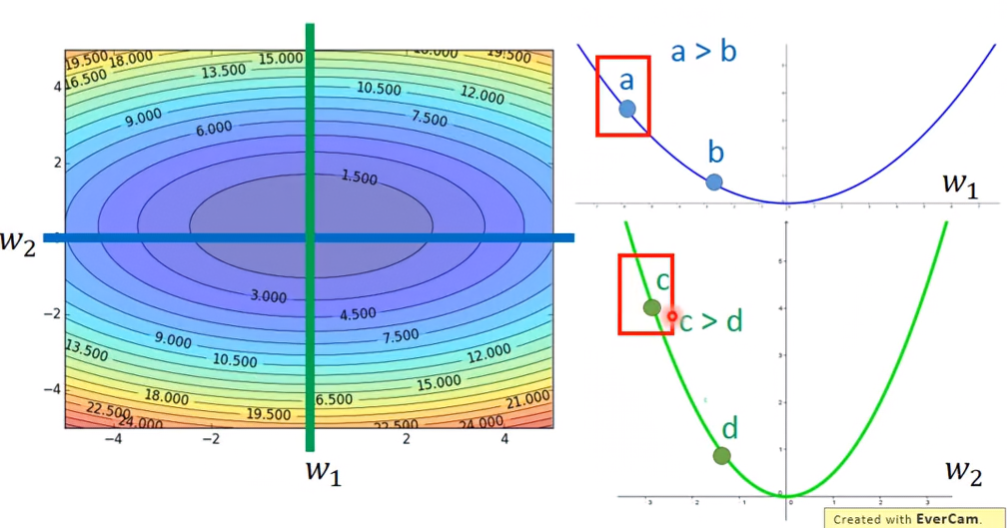
對圖形中間切橫線，可以得出 $w_1$ 的函數，找出兩點a、b，可以發現a點導數較大，其與最低點的距離也較長；對圖形中間切豎線，可以得出 $w_2$ 的函數，找出c、d兩點，可以發現c點導數較大，其與最低點的距離也較長。

當跨參數考慮導數值時，可以發現 $w_2$ 的函數切口比 $w_1$ 的函數來的尖，因此c點導數會比a點大，但事實上a點到最低點的距離是比c點遠的。所以在gradient descent時，如果只考慮一次微分的大小，那找出的點不會是最低點。

總結

我們看回單變數二次函數，某點對最低點的數學式：

|x_0+\frac{b}{2a}|=\frac{|2ax_0+b|}{2a}

上面已經提過了，分子是一次微分函數，那分母呢？

\frac{\partial^2 y}{\partial x^2}=2a

可以發現分母竟然是二次微分函數。

所以得知，一次微分函數除以二次微分函數做調整後，得到的結果才能反映在考慮多參數導數下的真正的比較結果。總結來說，當我們要考慮多參數函數在目前位置到最低點的距離時，要使用以下值做參考：

\frac{|First \space derivative|}{Second \space derivative}

Adagrad - View back to the formula

看回原本Adagrad在梯度下降的公式：

w^{t+1}=w^t-\frac{\eta}{\sqrt{\sum_{i=0}^{t}(g^i)^2}}g^t

會發現分母不是二次微分函數!? 但其實分母是跟二次微分函數有關的！

當今天模型很複雜時，可能算個一次偏導就要耗費很久的時間了，再算二次偏導的話，總訓練模型的時間又更長了。所以adagrad使用root mean sqaured來代替second derivative，可以省掉許多運算時間。

Explanation of root mean squared value

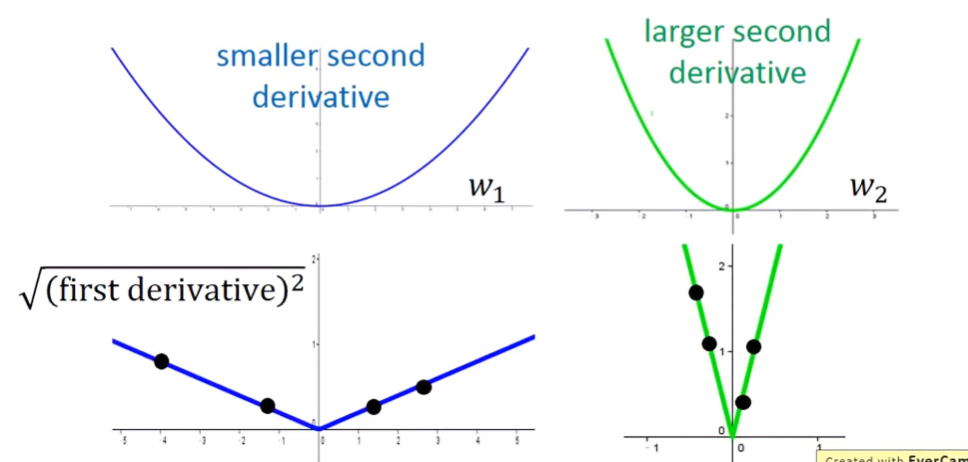
從下方圖形來看， $w_1$ 開口較平坦、 $w_2$ 開口較尖銳，對兩函數做一次微分。可以發現當今天sample夠多點時，在相同的x值下， $w_2$ 的一次偏導會比 $w_1$ 的還大，所以分母會比 $w_1$ 還大，能有效把 $w_2$ 高估的值拉下來。因此，使用root mean squared value校正的效果跟二次微分函數是一樣的。

Stochastic Gradient Descent

此法是專注於loss function計算的方法。一般loss function的數學式為：

L=\sum_n(\hat y - (b+\sum w_ix_i^n))^2

此loss function是一次算所有example的訓練值與真實值之差的總和，但Stochastic Gradient Descent是將每個example的loss分開算，所以第n個example，其loss為：

L^n=(\hat y^n-(b+\sum w_ix_i^n))^2

所以每次迭代時update的值就會從左式變右式：

\theta^i=\theta^{i-1}-\eta\nabla L(\theta^{i-1})

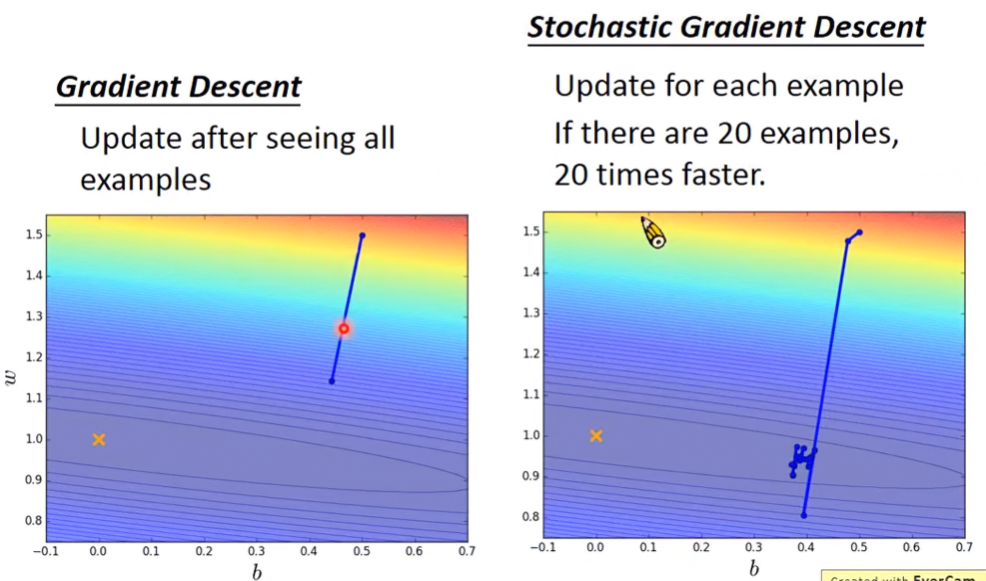
\theta^i=\theta^{i-1}-\eta\nabla L^n(\theta^{i-1})

從圖形來看，可以發現Stochastic比一般法跑得還快。Stochastic是每看到一個example就update一次參數；原本的方法是看完所有example才update一次參數。Stochastic只看一個example的話，步伐是小的、散亂的、不一致的，但因為能看很多個example，所以整體來說是比一般法來的快。

Feature Scailing

Introduction

假設現在有兩參數要做regression

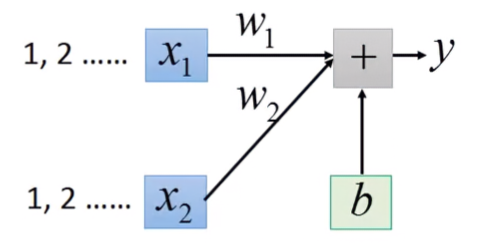
y=b+w_1x_1+w_2x_2

若兩參數分布的range很不一樣，就建議做rescaling，使得兩參數的分布能夠一樣

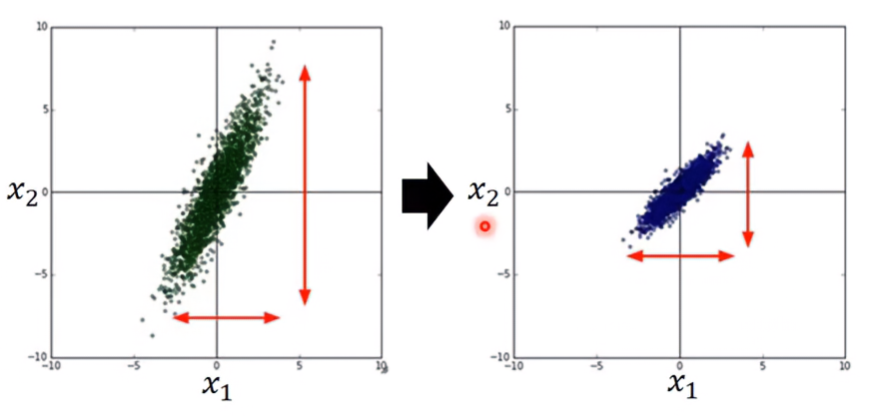
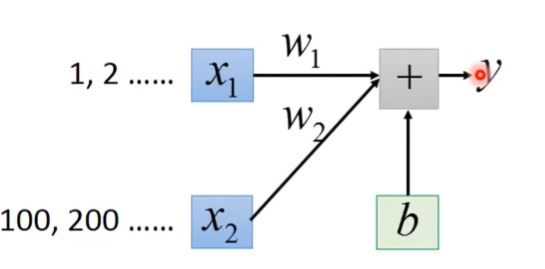
舉個例子，假設 $x_1$ 輸入的參數是1, 2, ……， $x_2$ 輸入的參數是100, 200, ……，則只要有較小的 $w_2$ 就能大幅度的影響y；要有較大的 $w_1$ 才能影響y。

如果視覺化來看，圖形會像個橢圓一樣；做完scaling之後，圖形就會像個圓形。從圖上可以發現橢圓形的圖不像圓形的圖，只要向圓心走就能到達最低點。橢圓的圖還須經過幾次折返才能到達最低點。

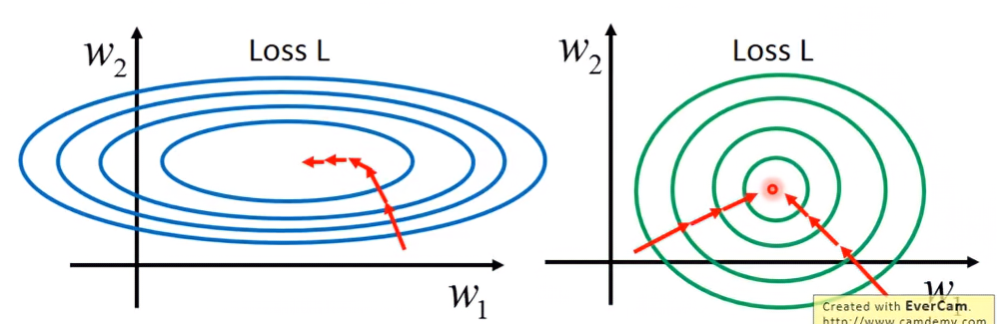
Practical method

假設有R個example: { $x^1,x^2,x^3,...,x^r,...,x^R$ }，每一筆example都有一組feature。

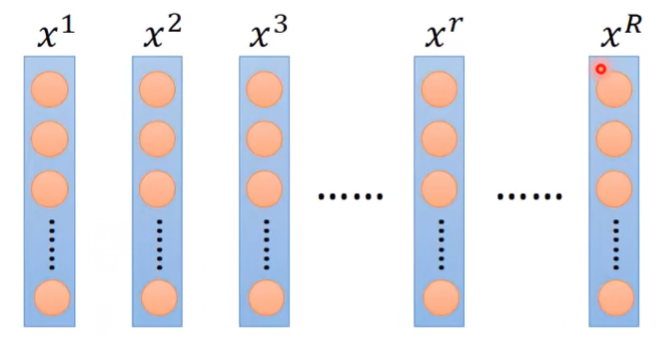
對第 i 個dimention的所有example取平均值 $m_i$ ，以及標準差(standard deviation) $\sigma_i$

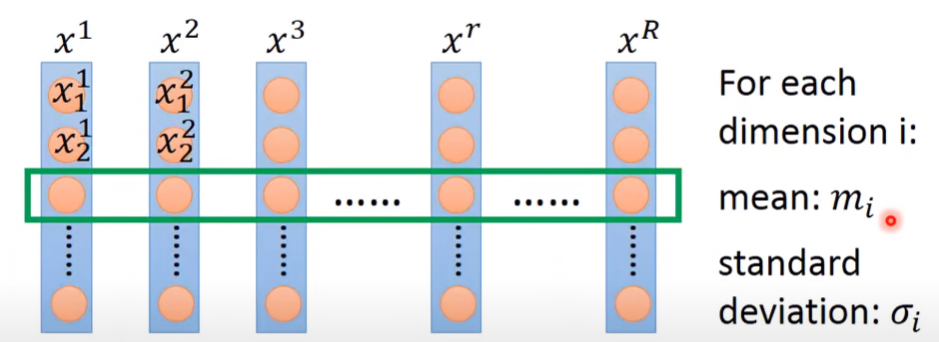
對第r個example的第i個參數 $x_i^r$ 減掉平均值再除以標準差
$x_i^r \longleftarrow \frac{x_i^r-m_i}{\sigma_i}$

如此做完localization之後，會發現所有dimention的平均值變為0，variance變為1。

Gradien Descent Theory

此章解釋Gradient Descent為什麼行的通？為什麼公式長那樣？

Taylor Series

單變數泰勒展開

令h(x)是在 $x=x_0$ 周圍為無窮可微函數，因此h(x)之泰勒展開為

h(x)=\sum^\infin_{k=0}\frac{h^{(k)}(x_0)}{k!}(x-x_0)^k \\ =h(x_0)+h'(x_0)(x-x_0)+\frac{h''(x_0)}{2!}(x-x_0)^2+...

當x足夠靠近 $x_0$ 時，則h(x)可省略高次項

h(x)\approx h(x_0)+h'(x_0)(x-x_0)

多變數泰勒展開 - 以雙變數x, y為例

令h(x,y)是在 $x=x_0, y=y_0$ 周圍為無窮可微函數，因此h(x,y)之泰勒展開為

h(x,y)=h(x_0,y_0)+ \frac{\partial h(x_0,y_0)}{\partial x}(x-x_0)+ \frac{\partial h(x_0,y_0)}{\partial y}(y-y_0) \\ +\space something \space related \space to \space (x-x_0)^2 \space and \space (y-y_0)^2+......

當 x, y 足夠靠近 $x_0,y_0$ 時，則高次項可省略成

h(x,y) \approx h(x_0,y_0)+\frac{\partial h(x_0,y_0)}{\partial x}(x-x_0) + \frac{\partial h(x_0,y_0)}{\partial y}(y-y_0)

Find the minimum in a circle in a contour field

Introduction

假設有兩參數 $\theta_1,\theta_2$ 與Loss function $L(\theta_1, \theta_2)$ 形成等高線場，求得在以某點 (a,b) 為圓心形成的圓圈中，其最小的Loss值

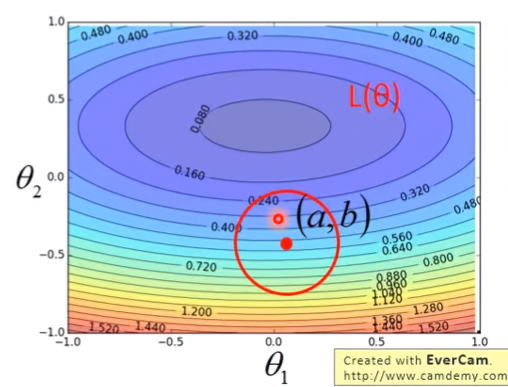
Proof

將Loss function以泰勒展開式表示，並假設此圓圈足夠小，小到Loss function在省略二次項以後的高次項後，仍足以近似圓圈內各點的Loss值。

設 (a , b) 為圓心， $(\theta_1,\theta_2)$ 為圓圈中某點，則

L(\theta)\approx L(a,b)+\frac{\partial L(a,b)}{\partial \theta_1}(\theta_1-a)+ \frac{\partial L(a,b)}{\partial \theta_2}(\theta_2-b)

設

s=L(a,b),\space u=\frac{\partial L(a,b)}{\partial \theta_1},\space v=\frac{\partial L(a,b)}{\partial \theta_2} \\ \Delta \theta_1=\theta_1-a,\space \Delta \theta_2=\theta_2-b

則Loss function可簡化為

L(\theta) \approx s+u\Delta\theta_1+v\Delta\theta_2

假設圓圈半徑為d，則條件限制為

\Delta\theta_1^2+\Delta\theta_2^2\leq d^2

因為 $(u,v),(\Delta\theta_1,\Delta\theta_2)$ 可視為從圓心點出發之向量，所以若不考慮初始值s的情況下，Loss function可被視為此二向量之內積和

L(\theta)= \begin{bmatrix} u & v \end{bmatrix} \cdot \begin{bmatrix} \Delta\theta_1 \\ \Delta\theta_2 \end{bmatrix}

因此， $(u,v),(\Delta\theta_1,\Delta\theta_2)$ 可以被視為從圓心點向外射出的向量，若要使Loss最小，則兩項之內積核應為0

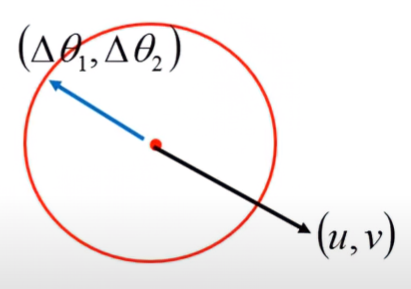
所以，兩向量互為反方向，且值的大小差了 $\eta$ 倍

\begin{bmatrix} \Delta\theta_1 \\ \Delta\theta_2 \end{bmatrix} =-\eta \begin{bmatrix} u \\ v \end{bmatrix} \\\Rightarrow\begin{bmatrix} \theta_1-a \\ \theta_2-b \end{bmatrix} =-\eta \begin{bmatrix} u \\ v \end{bmatrix} \\\Rightarrow\begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix} =\begin{bmatrix} a \\ b \end{bmatrix} -\eta \begin{bmatrix} u \\ v \end{bmatrix}

最後就可以得出Gradient Descent公式

\begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix} = \begin{bmatrix} a \\ b \end{bmatrix} -\eta \begin{bmatrix} \frac{\partial L(a,b)}{\partial\theta_1} \\ \frac{\partial L(a,b)}{\partial\theta_2} \end{bmatrix}

Condition Constraints of Gradient Descent

公式成立的前提是圓圈半徑要足夠小，意指learning rate $\eta$ 要夠小。若learning rate太大，會使估計函數不夠近似原loss function，導致學習成效不夠好( 如同上面Learning Rate章節一開始所說的 )。因此，理想條件是

\eta\rightarrow0

Limitation of Gradient Descent

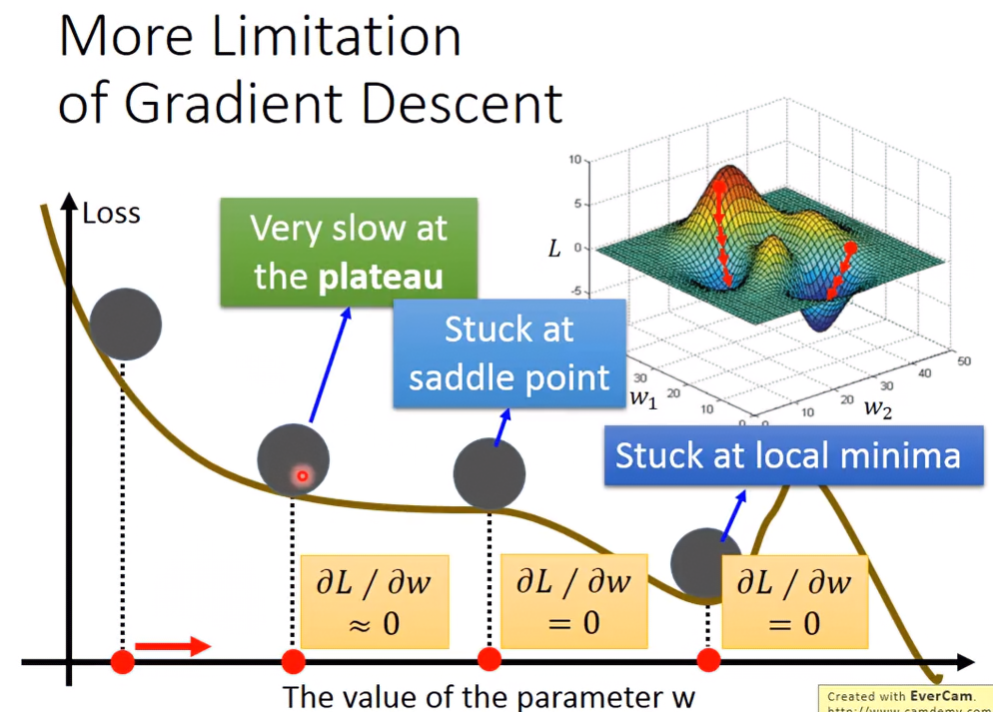
雖然梯度下降法可以快速找到較佳loss，但還是有其缺陷之處。如果碰到了一個非convex的函數，就會有「找到的minimum是local minimum而非global minimum」的問題。

還有因為我們都靠寫程式去做ML的，當碰到有一點斜率超級小但不為0時，電腦會因浮點數記憶體的限制，將非常小的數視為0，讓你以為找到了minimum，但其實有可能找出來的點非global minimum更非local minimum。

或是在高原時，斜率也會是0，這時找到的也不是minimum，反而是maximum。

Lecture 4: Classification

將資料分類，以便後續訓練時能有更好的效果。常見的分類應用有：

Credit Scoring
- Input: income, savings, profession, age, past finantial history, …
- Output: accept or refuse ( Binary Classification )

Medical Diagnosis
- Input: current symptoms, age, gender, past medical history, …
- Output: which kind of diseases

Classification as Regression?

可以使用regression來解決分類問題嗎？先來看一個例子：

Binary classification as example

Training: Class 1 means the target is 1; Class 2 means the target is -1

Testing: closer to 1 ⇒ class 1; closer to -1 ⇒ class 2

當資料有離群值時，則取線就會像紫色的那樣，會分類錯誤。

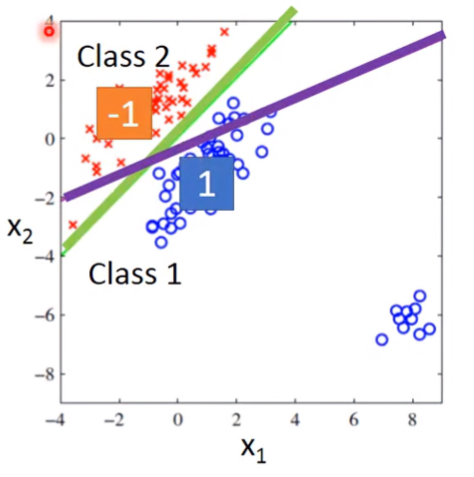
問題點：

It’ll penalize to the examples that are “too correct”

If we have multiple class: Class 1 means the target is 1; Class 2 means the target is 2; Class 3 means the target is 3, ……problematic
- 從數學圖形上來看，Class 1和Class 2是有關聯的；Class 2和Class 3是有關聯的。但實際上這些類別可能都是獨立的，這會導致分類錯誤。

💡

總結：不建議使用Regression解決Classification問題。

Ideal Alternatives

Function(Model)
- 設f(x)為離散函數，且f(x)為g(x)的函數：
$f(x)= \left\{ \begin{array}{c} g(x)>0 ,\space Output=class \space 1 \\ else ,\space\space\space\space\space\space\space\space\space Output=class\space 2 \end{array} \right.$

Loss function
- 為分類錯誤次數的總和
$L(f)=\sum_n \delta(f(x^n)\neq\hat y^n)$

Find the best function
- 因為L是離散函數，無法微分，不能使用Gradient Descent，所以可以用以下方式找最佳解
- Example: Perceptron, SVM

Classification: Probabilistic Generative Model

假設有個分類問題，要根據寶可夢的7個維度的資料Total, HP, Attack, Defense, SP Atk, SP Def與Speed，去分類此寶可夢是水系還是一般系？

我們也許可以找出某寶可夢為某類別的機率，再根據條件，像是機率>0.5代表為水系，來做分類。以下為機率推導示範。

Two Classes

假設水系類別為 $C_1$ ，一般系類別為 $C_2$ ，指定的寶可夢為x，則：

$P(C_1)$ ：從水系類的寶可夢裡挑出一隻寶可夢的機率

$P(C_2)$ ：從一般系的寶可夢裡挑出一隻寶可夢的機率

$P(x|C_1)$ ：從水系類的寶可夢找到x的機率

$P(x|C_2)$ ：從一般系的寶可夢找到x的機率

有了以上的數值，我們就可以找出x為某類別的機率。假設想找出x為水系的機率：

P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}

這是根據貝式定理推導出來的，分子是「樣本屬於 $C_1$ 類別且觀察到x的機率 ( $P(x\cap C_1)$ ) 」，分母是Generative Model，也是觀察到x的總機率，使用全機率定理推導。

$P(C_1),P(C_2)$ 可以很容易得到，只要將該類別寶可夢數除以母體樣本總數即可得到，但 $P(x|C_1),P(x|C_2)$ 的推導就比較複雜了，以下用Guassion Distribution說明。

Guassion Distribution

What is Guassion Distribution?

高斯分布被作為最常見的連續隨機變量的機率分布，我們可以透過 $\mu,\Sigma$ 變數控制高斯分布的場，離場中心點越進，則發生在此區的事件機率越高；離場越遠，則在事件發生機率越小，但不會為0。

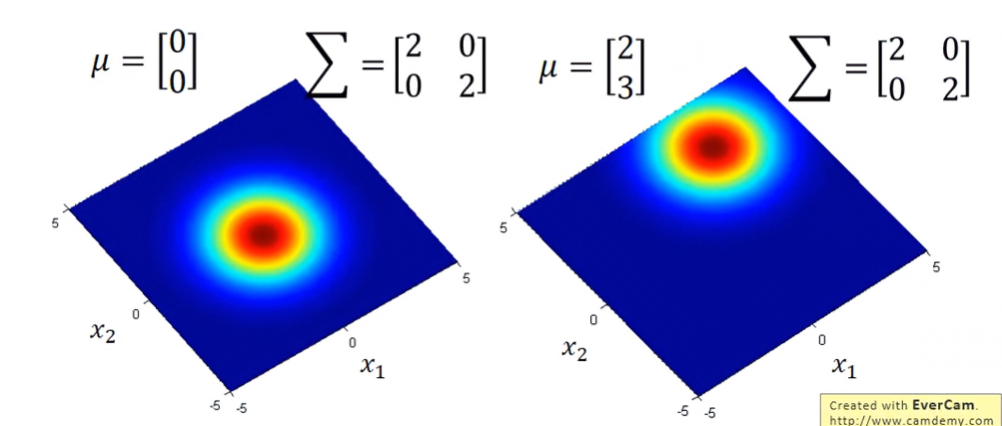
$\mu$ ：mean。所有樣本數的平均值，是個vector。用來控制機率分布最高點的地方，如上圖在不同的 $\mu$ ，相同的 $\Sigma$ 下，兩圖分布的最高點位置不同。

$\Sigma$ ：covariance matrix。衡量隨機變數間的相關程度，是個matrix。如下圖在相同的 $\mu$ ，不同的 $\Sigma$ 下，兩圖分布的最高點位置一樣，但分布程度不同。

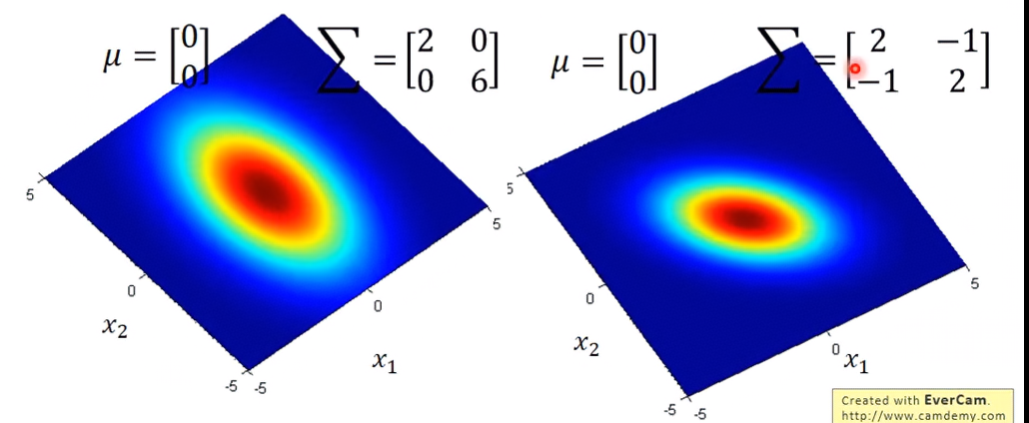
如果要求x事件在某高斯分布場發生的機率密度，則公式如下：

f_{\mu,\Sigma}(x)=\frac{1}{(2\pi)^{\frac{D}{2}}} \frac{1}{|\Sigma|^{\frac{1}{2}}} \exp \left\{ -\frac{1}{2} (x-\mu)^T \Sigma^{-1} (x-\mu) \right\}

How to find $\mu,\Sigma$ ：Maximum Likelihood

假設手上有140筆寶可夢資料，有79個是水系，61個是一般系。若將水系寶可夢的Defense跟SP Defense參數提取當參考，則這79之寶可夢的分布圖形如下：

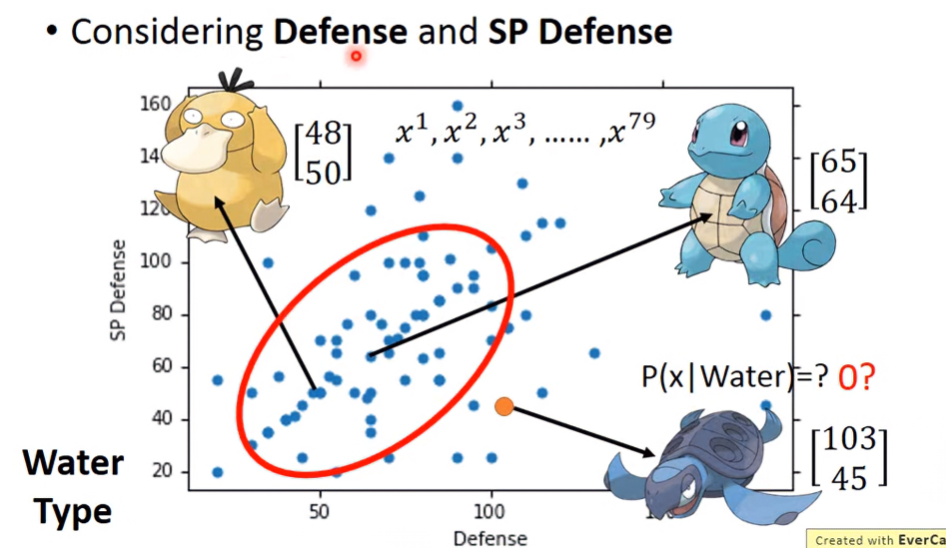
我們可以想像，任何一個Space的Gaussian都有可能取樣這79個點，只是差在這79個點的機率大小而已，這種在某一Space的Gaussian取樣這些點的可能性被稱為Likelihood。那這樣我們到底要取哪個高斯分布場，才能最精準的描述資料的分布狀況？

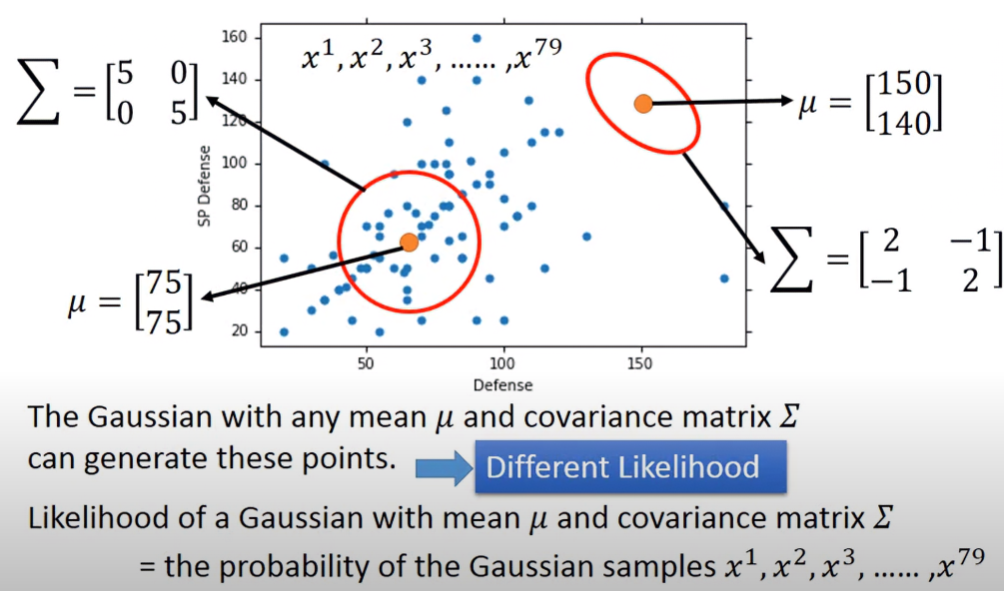
在某一Space的Gaussian取樣所有樣本的可能性Likelihood，其計算方式就是把所有樣本的Gaussian機率相乘。因為要有這likelihood等於是所有樣本事件都要在此高斯分布場下發生，自然而然likelihood就是所有事件的高斯機率相乘。

L(\mu,\Sigma)=f_{\mu,\Sigma}(x^1) f_{\mu,\Sigma}(x^2) f_{\mu,\Sigma}(x^3) \times......\times f_{\mu,\Sigma}(x^{79})

如果要找最佳的高斯分布場，也許可以對L作微分取極值，但這樣太麻煩了。假設我們有maximum likelihood的高斯分布場 $(\mu^*,\Sigma^*)$ ，並從中找出了資料 $x^1,x^2,x^3,......,x^{79}$ ，則可以這樣計算：

\mu^*,\Sigma^*=\arg\max_{\mu,\Sigma}L(\mu,\Sigma) \\ \mu^*=\frac{1}{79}\sum^{79}_{n=1}x^n \\ \Sigma^*=\frac{1}{79}\sum^{79}_{n=1}(x^n-\mu^*)(x^n-\mu^*)^T

View back to the problem

所以我們可以透過兩類別的樣本計算出各自的高斯分布 $(\mu^1,\Sigma^1),(\mu^2,\Sigma^2)$ ，接下來就可以算出我們想要的機率：

P(x|C_1)= f_{\mu^1,\Sigma^1}(x)=\frac{1}{(2\pi)^{\frac{D}{2}}} \frac{1}{|\Sigma^1|^{\frac{1}{2}}} \exp \left\{ -\frac{1}{2} (x-\mu^1)^T (\Sigma^1)^{-1} (x-\mu^1) \right\}

P(x|C_2)= f_{\mu^2,\Sigma^2}(x)=\frac{1}{(2\pi)^{\frac{D}{2}}} \frac{1}{|\Sigma^2|^{\frac{1}{2}}} \exp \left\{ -\frac{1}{2} (x-\mu^2)^T (\Sigma^2)^{-1} (x-\mu^2) \right\}

上面機率值代回公式計算 $P(C_1|x)$

所以：

P(C_1|x) \gt 0.5 \Rightarrow x\space belongs \space to \space class \space 1

Result

只考慮Defence跟SP Defence的話，可以看到下圖，正確率只有47%。若將寶可夢所有7個維度的參數都考慮的話，正確率也只有54%，還不如直接用隨機猜的。所以接下來繼續探討原因跟解決方法。

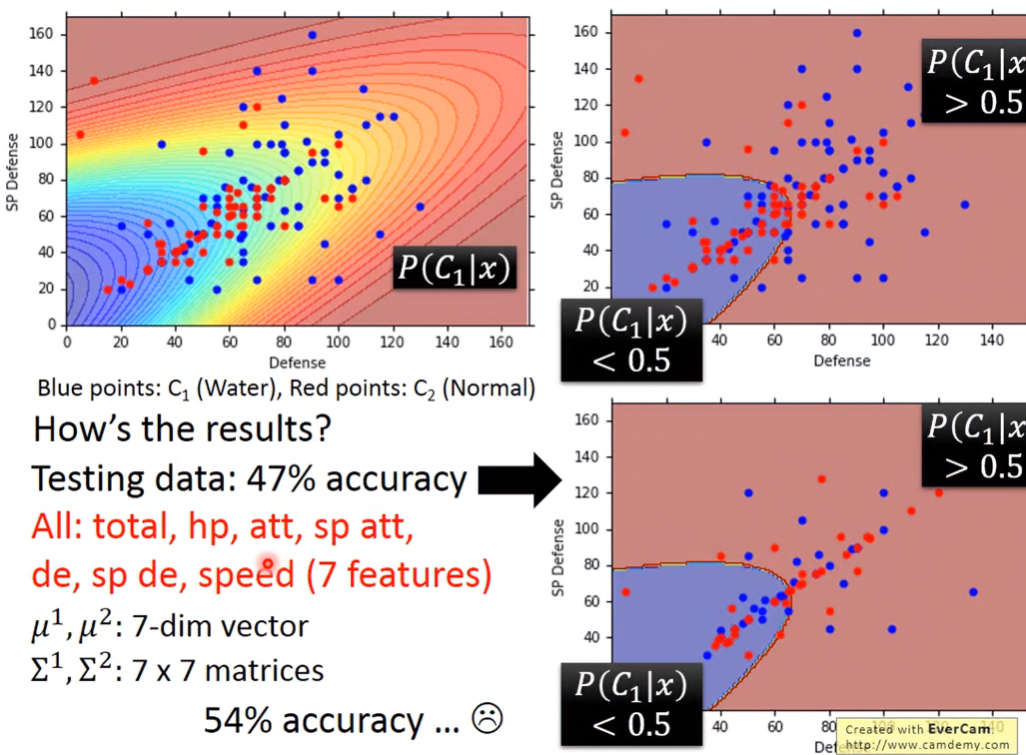
Modifying Model

上一章的Model是每個Class的Gaussian都有自己的mean跟covariance matrix，但這其實是比較少見的。比較常見的做法是所有Class的Gaussian都共用同一個covariance matrix，這是因為：

Covariance Matrix size跟input data的feature數量成平方正比

如果每個model都有自己的covariance matirx，這樣參數就太多了，會導致variance變大，容易overfitting

Calculate the common covariance matrix

假設一樣是兩組資料，分別為水系跟一般系。這兩組資料有各自的平均值，但使用的covariance matrix是相同的：

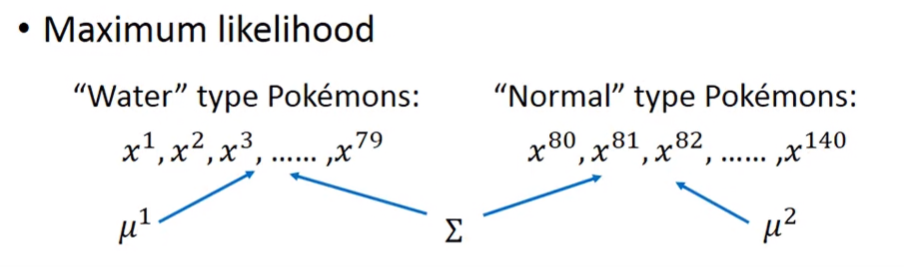
這樣的話，先考慮兩組資料的likelihood：

L(\mu^1,\mu^2,\Sigma)= f_{\mu^1,\Sigma}(x^1) f_{\mu^2,\Sigma}(x^2) \times......\times f_{\mu^{79},\Sigma}(x^{79}) \times......\times f_{\mu^{80},\Sigma}(x^{80}) f_{\mu^{81},\Sigma}(x^{81}) \times......\times f_{\mu^{140},\Sigma}(x^{140})

如果想要Maximizing Likelihood的話，兩組資料的mean的算法跟之前是一樣的：

\mu^1=\frac{1}{79}\sum^{79}_{n=1}x^n_1 \\ \mu^2=\frac{1}{61}\sum^{61}_{n=1}x^n_2

先算兩組資料個別的covariance matrix，再透過資料數比例，得出共用的covariance matrix：

\Sigma=\frac{79}{140}\Sigma^1+\frac{61}{140}\Sigma^2

可以看到共用了covariance matrix後，boundary變成線性的，其正確率從54%提升至73%。因為參考的是七維的feature，而圖形是二維的，所以從圖形上看不出什麼所以然，畢竟是從高維空間映射上去的。但在高維空間中，是有明確將大部分點分開的。

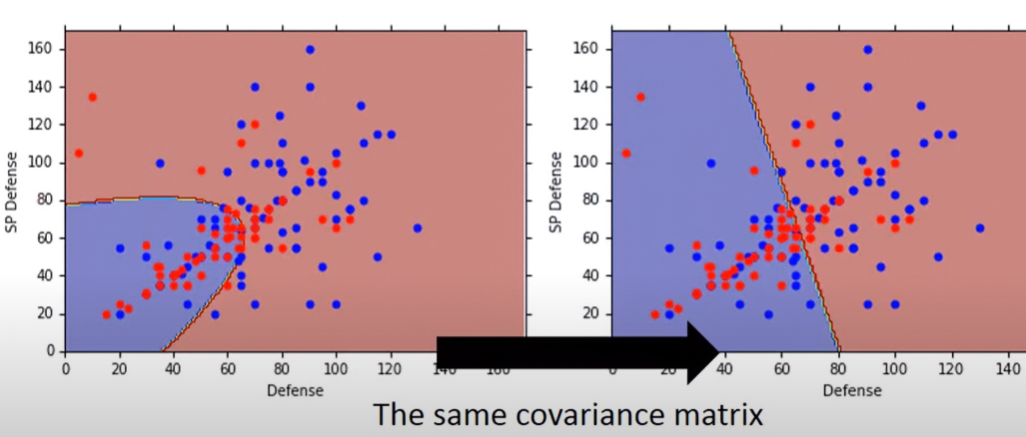
Three Steps

在前面Ideal Alternatives章節，有提到怎麼不用regression的步驟解決分類問題，現在我們把上面學到的機率概念也加進去。

Function Set (Model)：
$P(C_1|x)=\frac {P(x|C_1)P(C_1)} {P(x|C_1)P(C_1)+P(x|C_2)P(C_2)} \\ y= \left\{ \begin{array}{c} Class\space1,\space P(C_1|x)\gt0.5 \\ Class\space2,\space Otherwise\space\space\space\space\space\space \end{array} \right.$

Goodness of a function：
- The mean $\mu$ and covariance $\Sigma$ that maximizing the likelihood (the probability of generating data)

Find the best function：easy

Choose Probability Distribution Model

根據data set的特性、想求的目標，選擇適合的機率分布模型，可以有最好的分類效果，例如：

二元分類法
- Bernoulli distributions

所有的dimensions都是獨立的
- Naive Bayes Classifier

Posterior Probability

我們在「Classification: Probabilistic Generative Model」章節想找的 $P(C_1|x)$ 其實就是後驗機率(Posterior Probability)，指在已經觀察到某些資料x之後，某個事件或類別發生的機率。可以從貝式定理的公式，找出我們要的後驗機率。以下是後驗機率更深入的推導：

P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)} \\ =\frac{1}{1+\frac{P(x|C_2)P(C_2)}{P(x|C_1)P(C_1)}}\space\space\space\space\space\space\space\space\space\space\space\space\space\space \\ =\frac{1}{1+\exp{(-z)}}\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space \\ =\sigma{(z)}\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space

where\space z=\ln{ \frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2)} }

可以得知其時後驗機率就是z的sigmoid function。

而z可以作化簡：

z=\ln{ \frac{P(x|C_1)}{P(x|C_2)} }+ln{ \frac{P(C_1)}{P(C_2)} }

\because \frac{P(C_1)}{P(C_2)}=\frac{ \frac{N_1}{N_1+N_2} }{ \frac{N_2}{N_1+N_2} }

\therefore \ln{\frac{P(C_1)}{P(C_2)}}= \ln{ \frac{N_1}{N_2} }

在使用common covariance matrix( $\Sigma=\Sigma^1=\Sigma^2$ )的前提下，z經過複雜的運算，推導的結果為：

z = (\mu^1 - \mu^2)^T \Sigma^{-1} x - \frac{1}{2} (\mu^1)^T \Sigma^{-1} \mu^1 + \frac{1}{2} (\mu^2)^T \Sigma^{-1} \mu^2 + \ln \left( \frac{N_1}{N_2} \right)

這項數學式被拆分成兩部份後，可被視為一個線性方程式，其中：

w^T=(\mu^1-\mu^2)^T\Sigma^{-1}

b=-\frac{1}{2}(\mu^1)^T(\Sigma^1)^{-1}\mu^1+ \frac{1}{2} (\mu^2)^T(\Sigma^2)^{-1}\mu^2+ \ln{\frac{N_1}{N_2}}

則：

z=w\cdot x+b

所以後驗機率可被表示為線性方程式：

P(C_1|x)=\sigma{(w\cdot x+b)}

總結

在Generative model，只要有 $N_1,N_2,\mu^1,\mu^2,\Sigma$ ，就可以算出 $w,b$ ，以此算出後驗機率，完成分類器的實作。
但是，這樣去算
$w,b$ 會不會太複雜？我們能不能用更簡單的方式去計算呢？下一個Lecture將提到這件事情。

*補充

S型函數 ( Sigmoid Function )

Sigmoid function又被稱為S型函數，因為其輸出0到1之間的非線性函數，圖形看起來像一個平滑的「S」。當 $z\rightarrow+\infty$ ，輸出趨近於1；當 $z\rightarrow-\infty$ ，輸出趨近於0。
其函數為：

\sigma{(z)}= \frac{1}{1+e^{-z} } \space where \space z \in\real

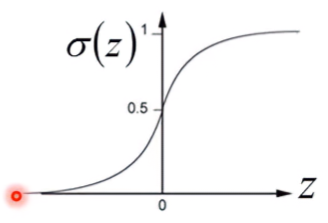
似然比 ( Likelihood Ratio )

來源於後驗機率：

z=\ln{ \frac{P(x|C_1)}{P(x|C_2)} }+ln{ \frac{P(C_1)}{P(C_2)} }

其中的：

\ln{ \frac{P(x|C_1)}{P(x|C_2)} }

這個比例的意義在於，根據資料x在各類別下的機率，判斷它更像哪一類。

先驗比（Prior Ratio）

來源於後驗機率：

z=\ln{ \frac{P(x|C_1)}{P(x|C_2)} }+ln{ \frac{P(C_1)}{P(C_2)} }

其中的：

ln{ \frac{P(C_1)}{P(C_2)} }

這個比例的意義在於，表示事先對各類別的偏好（像是在 spam 濾信時，垃圾信的機率本來就比較高）。