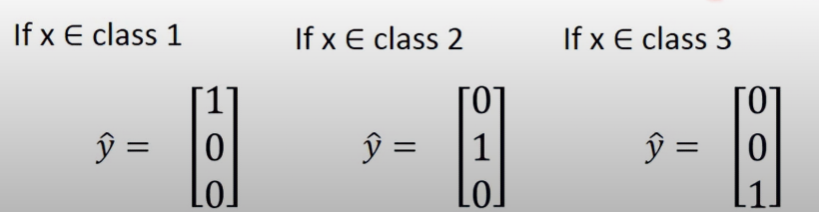Lecture 5: Logistic Regression
Step 1: Function Set
上一張提到分類問題,我們把這問題以機率模型解決:
y={C1, Pw,b(C1∣x)≥0.5C2, Otherwise 根據重重推導,我們發現此機率可被簡化為sigmoid function:
Pw,b(C1∣x)=σ(z) 此sigmoid function的變數z為一線性模型:
z=w⋅x+b=i∑wixi+b 當我們使用不同的w, b參數,就會得到不同的後驗機率。假設我們觀察到事件x,其在所有不同w, b參數下,發現為 C1 類別的機率,可以形成一個function set:
fw,b(x)=Pw,b(C1∣x) where w,b∈ℜ 以圖形化來看,會長這樣:
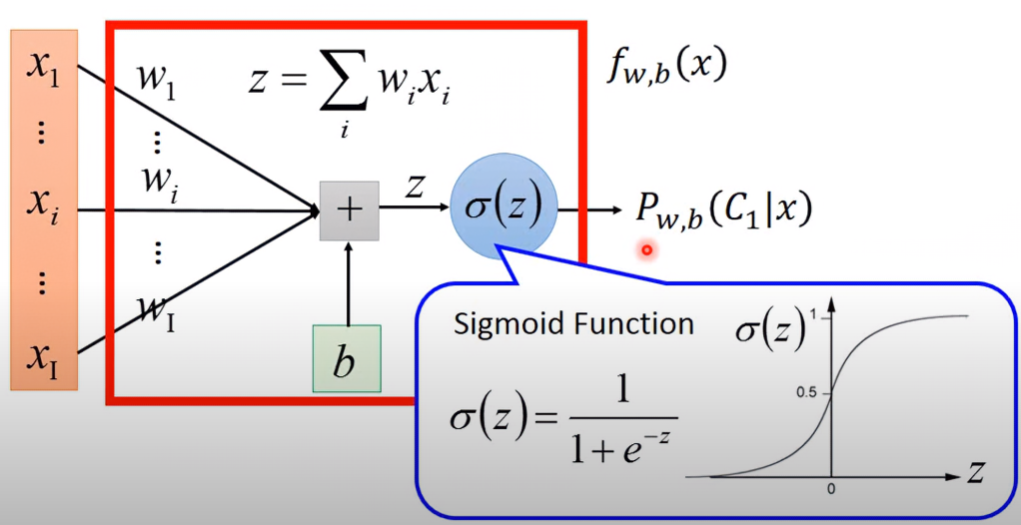
訓練這模型的過程,可以被稱為Logistic Regression
Step 2: Goodness of a Function
Assumption and Derivation
Traning Data會有Class 1的資料,也會有Class 2的資料:
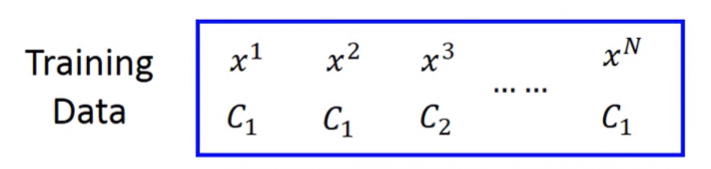
假設這些資料都在某高斯場產生,而每筆資料在這高斯場發生的機率為:
fw,b(x)=Pw,b(C1∣x) 對於某組給定的w和b,全部資料在此高斯場發生的可能性為:
L(w,b)=fw,b(x1)fw,b(x2)(1−fw,b(x3))⋅......⋅fw,b(xN) 令發生在可能性最高的高斯場,其參數為 w∗,b∗:
w∗,b∗=argw,bmaxL(w,b)=argw,bmin−lnL(w,b) 可以發現上述數學式將取max換成取min,所以多加了負號。然後再對L取natural log,這對結果不影響,所以左右兩式的等號成立,但可以從連乘變為連加,使得計算更簡易。對於L取natural log,可以再進一步推導:
−lnL(w,b)=−lnfw,b(x1)−lnfw,b(x2)−ln(1−fw,b(x3))+...... 這裡可以發現,因為不是所有資料都是Class 1的,所以屬於Class 2的項都要以 1−fw,b 來表示。資料類別的不確定性,導致 −lnL(w,b) 的數學式推導不能以連加來公式化,因此這裡引進了delta function的概念:
y^n={1, for class 10, for class 2 把 −lnL(w,b) 裡的所有項以 y^n 的線性組合表示:
−lnL(w,b)=−[y^1lnf(x1)+(1−y^1)ln(1−f(x1))]−[y^2lnf(x2)+(1−y^2)ln(1−f(x2))]−[y^3lnf(x3)+(1−y^3)ln(1−f(x3))]+...... 這下就可以用sigma整理:
−lnL(w,b)=n∑−[yn^lnfw,b(xn)+(1−y^n)ln(1−fw,b(xn))] 仔細發現的話,其實這數學式是兩個Bernoulli distribution之間的Cross entropy:
Distribution p ;
p(x=1)=y^np(x=0)=1−y^n Distribution q :
q(x=1)=f(xn)q(x=0)=1−f(xn) 而 −lnL(w,b) 其實就是兩個分布的交叉熵 H(p,q):
−lnL(w,b)=H(p,q)=−x∑p(x)ln(q(x)) Conclution
定義交叉熵函數 C(f(xn),y^n) 為:
C(f(xn),y^n)=−[y^nlnf(xn)+(1−y^n)ln(1−f(xn))] 當Training data為 (xn,y^n) 時,因為cross entropy的意義在於兩分佈有多接近,若兩分佈一模一樣的話,則cross entropy為極小值。在logistic regression中,Loss function就是所有資料的likelihood與 y^n的交叉熵總和:
L(f)=n∑C(f(xn),y^n) 💡
此處 f(xn),y^n 皆為Bernoulli distribution
Step 3: Find the best function
Preview
fw,b(x)=σ(z)=1+exp(−z)1 z=w⋅x+b=i∑wixi+b Derivation: Find Gradient Descent
求Loss function能有最小loss ⇒ 使用反向梯度,對Loss function求偏導:
∂wi∂(−lnL(w,b))=∂wi∂{∑n−[y^nlnfw,b(xn)+(1−y^n)ln(1−fw,b(xn))])} =n∑−[y^n∂wi∂(lnfw,b(xn))+(1−y^n)∂wi∂(ln(1−fw,b(xn)))] 兩個偏導項先分開處理
求前項偏微分推導
∂wi∂lnfw,b(x)=∂z∂lnfw,b(x)∂wi∂z 先處理後項:
∂wi∂z=∂wi∂(wi⋅xi+b)=xi 再處理後項:
∂z∂lnfw,b(x)=∂z∂lnσ(z)=σ(z)1∂z∂σ(z)=σ(z)1σ(z)(1−σ(z))=1−σ(z) 所以:
∂wi∂lnfw,b(x)=xi(1−σ(z))=xi(1−fw,b(xn)) 求後項偏微分推導
∂wi∂ln(1−fw,b(x))=∂z∂ln(1−fw,b(x))∂wi∂z 後項已知是 xi,推導前項:
∂z∂ln(1−σ(z))=−1−σ(z)1∂z∂σ(z)=−1−σ(z)1σ(z)(1−σ(z))=σ(z) 所以:
∂wi∂ln(1−fw,b(x))=xiσ(z)=xifw,b(xn) 繼續推導原公式
∂wi∂(−lnL(w,b))=n∑−[y^n∂wi∂(lnfw,b(xn))+(1−y^n)∂wi∂(ln(1−fw,b(xn)))] =n∑−[y^n(1−fw,b(xn))xin−(1−y^n)fw,b(xn)xin] =n∑−[y^n−y^nfw,b(xn)−fw,b(xn)+y^nfw,b(xn)]xin =n∑−(y^n−fw,b(xn))xin Conclution
在每次迭代時,更新的參數為:
wi+1←wi−ηn∑−(y^n−fw,b(xn))xin 從這可以看出w的update取決於三件事:
- y^n the ideal output
- 所以 (y^n−fw,b(xn)) 代表目前f的output與理想值的差距,當這差距越大, wi 更新的幅度越大
Logistic Regression v.s. Linear Regression
Logistic Regression
- Model:
Output: between 0 and 1
fw,b(x)=σ(i∑wixi+b)
- Iteration:
wi+1←wi−ηn∑−(y^n−fw,b(xn))xin
Linear Regression
- Model:
Output: any value
fw,b(x)=i∑wixi+b
L(f)=21n∑(f(xn)−y^n)2 - Iteration:
wi+1←wi−ηn∑−(y^n−fw,b(xn))xin
💡
Logistic Regression跟Linear Regression在參數的迭代上竟然相同!只差在其 f 的值域不同而已。
Why not Square Error?
雖然像linear regression的loss function那樣使用square error很方便、推導簡單,但是套用在logistic regression就不適合了。
從下圖可以看到在loss function較大時,使用交叉熵可以更反映某點在較大值時與最低點的陡斜程度,所以在每次迭代時可以更快找到最低點;如果使用square error的話,就會太過平坦了,在找最低點的速度就會極緩慢。

Discriminative v.s. Generative
後驗機率的公式,如果從不同角度切入,就會得到不同意義的結果,左半圖為Discriminative Model,右圖為Generative Model:

兩個Model的function set其實是一樣的,但兩個模型做了不同假設,所以同一組taining data得出的結果會不一樣。
- Discriminative Model:直接學習「輸入x屬於哪個類別y」的邊界或機率。
- 使用迭代,直接學習decision boundary
- 在數學上學的是「在已知特徵x的情況下,屬於類別y的機率」、「不會去建模 x 的分布」 P(y∣x)
- 只根據已知的 x 特徵,直接學習如何分類(或判斷 y),不對 x 的機率分布做任何假設
- 不關心每一類的樣本長什麼樣,只管怎麼把不同類分開,像是面試官,直接判斷你「該不該錄取」
- 常見例子:Logistic Regression、SVM、Neural Network
- Generative Model:學習「每個類別下,數據會長什麼樣」以及「每個類別本身的比例」。
- 算出Gaussion的 μ,Σ,估計每個類別下的參數
- 在數學上學的是「給定類別Y,數據x出現的機率,還有每個類別本身的機率」、「主動建模每個類別下 x 的分布」(P(x∣y),P(y))
- 先針對每一類型 y,估計 x 的機率分布(如 Gaussian 的 μ,Σ ),然後再根據這些分布來分類或生成樣本
- 關心每一類樣本的分布、特徵,像是專門分析各個公司的履歷特徵,知道各種背景的人大致長什麼樣子,再來算你比較像哪一種人
- 常見例子:Naive Bayes、Guassion Mixture Model、Hidden Markov Model、GAN
Example
有13組訓練資料,每組資料都有兩個dimention的元素,元素可能為1或0,每組資料的類別如下:
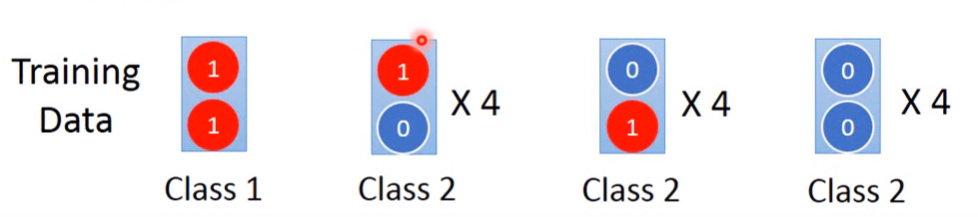
現在有一組測試資料,資料裡的兩個dimention值都是1,求此資料的類別可能會是?

Solve the problem
假設使用Generative Model,且每組資料的每個dimention都是獨立關係,因此挑選其資料分布為Naive Bayes:
P(x∣Ci)=P(x1∣Ci)P(x2∣Ci) 計算每個類別的參數:
P(C1)=131 P(C2)=1312 因為測試資料的兩個dimention都是1,設資料的第i個dimention為 xi,所以只要算從某類別抽出的 xi 是1的機率就好:
P(x1∣C1)=1 P(x2∣C1)=1 P(x1∣C2)=31 P(x2∣C2)=31 利用貝式定理求出觀察到某資料的所有dimention為1,其類別可能為 C1 的機率:
P(C1∣x)=P(x∣C1)P(C1)+P(x∣C2)P(C2)P(x∣C1)P(C1) ={P(x1∣C1)P(x2∣C1)}P(C1)+{P(x1∣C2)P(x2∣C2)}P(C2){P(x1∣C1)P(x2∣C1)}P(C1) =(1×1)×131+(131×131)×1312(1×1)×131=20291≪0.5 計算後可以得知此機率非常小,所以此資料為class 2。
Conclution of the result of the example
但看回訓練資料,可以發現Class 2的所有資料完全沒有兩個dimention值都是1的情況,所以這結果讓人感覺不是那麼直觀。會這樣是因為,一開始就假設所有dimention都是獨立的,使用了Naive Bayes機率分布模型描述資料。所以generative model就根據這假設,在參考所有類別的可能性後,自己腦補了結果,使得結果是訓練資料裡沒有被觀察到的現象。
Generative model這種腦補的行為,在訓練資料量不多時,相比Discriminative model能有較佳的結果。
- Benefit of generative model
- 由於確定了機率分布的假設,使得訓練資料量可以不用很多,且比較不會受資料的噪音影響
- 可以從不同的資料算出先驗機率( Priors probabilities,如: P(C1) )與類別依賴的機率( Class-dependent Probabilities,如: P(x∣C1) )
但當資料量夠多時Discriminative Model還是比Generative Model來的優。
Multi-Class Classfication
Previously on Softmax
在解決多類別的分類問題之前,先介紹一下Softmax。Softmax在本問題的解法擔任了關鍵的角色,以下為softmax的流程。
- 前提:每個類別樣本的高斯分布都共用同個covariance matrix
- 輸入資料:由n個類別方程式組成的向量
z=z1z2⋮zn
- 計算向量中每個參數取自然指數函數的值⇒取得所有值的總和⇒每個參數yi為函數值除以總和
yi=P(Ci∣x)=∑j=1nezjezi
- 輸出:由 n 個 yi 組成的向量
y=y1y2⋮yn
Softmax輸出向量每個參數都是機率,其特性有:
- ∑iyi=1
Solve the problem
對於多個類別的分類問題,可以用下面步驟解決:
- 訓練資料的每個類別都會有自己的權重向量與偏移量形成的線性方程。假設輸入資料是個d維的向量 x={x1,x2,.....,xd},總共有n個類別,則每個類別的方程式為
Class 1: z1=w1+b1Class 2: z2=w2+b2⋮Class n: zn=wn+bn
- 每個方程經過Softmax function運算後得到 yi,而yi就是每個類別的機率 fw,b(xn)
y1=Softmax(z1)y2=Softmax(z2)⋮yn=Softmax(zn)
- 對於所有類別的機率 yi,可以形成向量 y
y=y1y2⋮yn
- 有了每個類別的機率,接下就需要每個類別的target,也就是真實答案 y^i,其實就是delta function的概念
- 定義 y^ 是個包含所有類別真實答案的vector
y^=y^1y^2⋮y^n
- 如果 x∈Class j,則 y^j=1,然後 y^i=0 ∀ i=j:
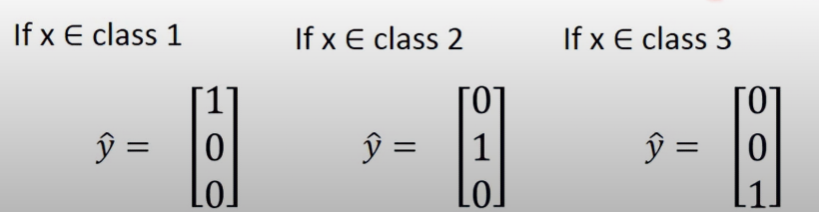
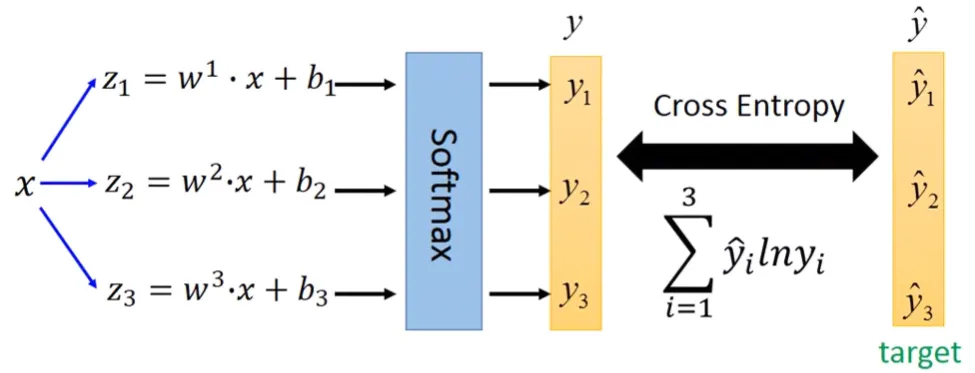
- 向量 y 與向量 y^ 的交叉熵就是Loss function
L(y)=−n∑y^ilnyi
- 最後照著Logistic Regression的方式去minimize cross entropy (=minimize loss function=maximize likelihood),就可以解決多類別的分類問題
Limitation of Logistic Regression
Introduction
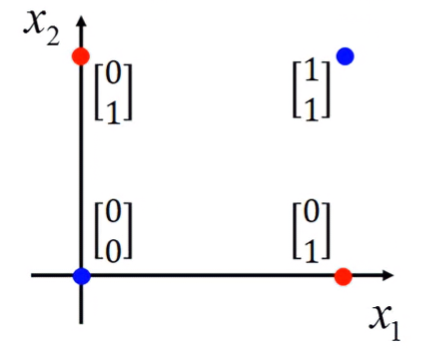
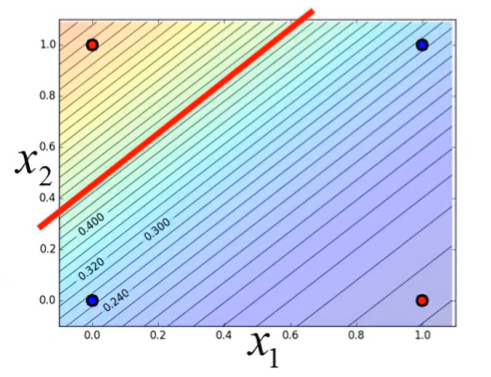
因為Logistic Regression的Boundary是一條直線,假設資料的分佈長這樣,則不管boundary在哪裡,都無法完美地分類:
解決方法就是把資料換到另一個space上,以下以範例說明。
Example
假設有四組資料,每組資料都有兩個特徵:
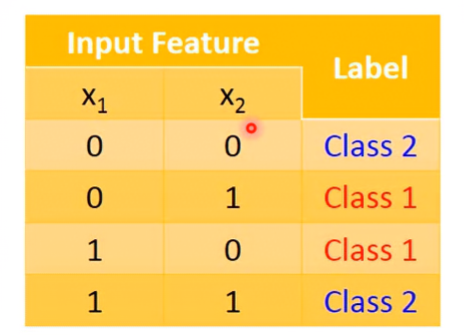
其方程式為:
y=σ(z) where z=w1x1+w2x2+b 在Introduction中,我們可以看到因為boundary為一條直線,而feature的分佈使得這條直線無法完美分類。若要解決此問題,就要將資料換到另一個space,使得:
{Class 1, y≥0.5Class 2, y<0.5 而轉換的方法被稱為 Feature Transformation
Feature Transformation: Cascading logistic regression models
Introduction
有很多種特徵轉換的方法,但比較簡單、常見的做法是串接多個logistice regression模型的加權組合,並產生新的輸出:
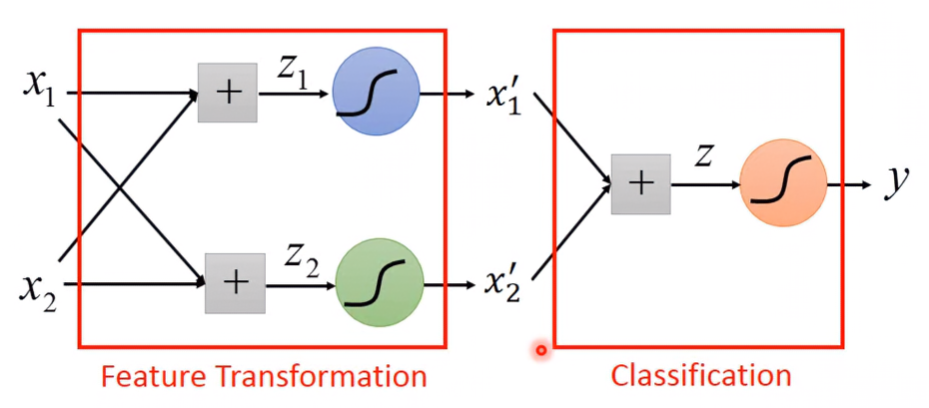
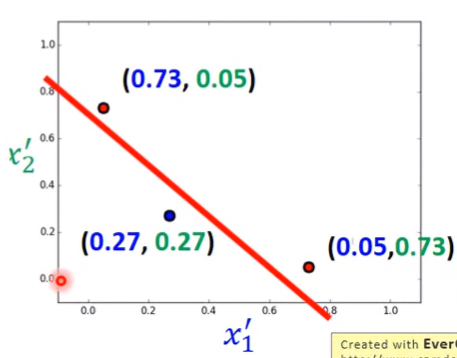
上述範例的 x1,x2 經過特徵轉換後變成新的 x1′,x2′ ,其轉換方程式為(塗上少了每個特徵的獨立權種與偏移):
[x1′x2′]=σ([w11w21w12w22][x1x2]+[b1b2]) Apply to the example
把特徵轉換套用到範例後,會發現boundary可以完美分類data。
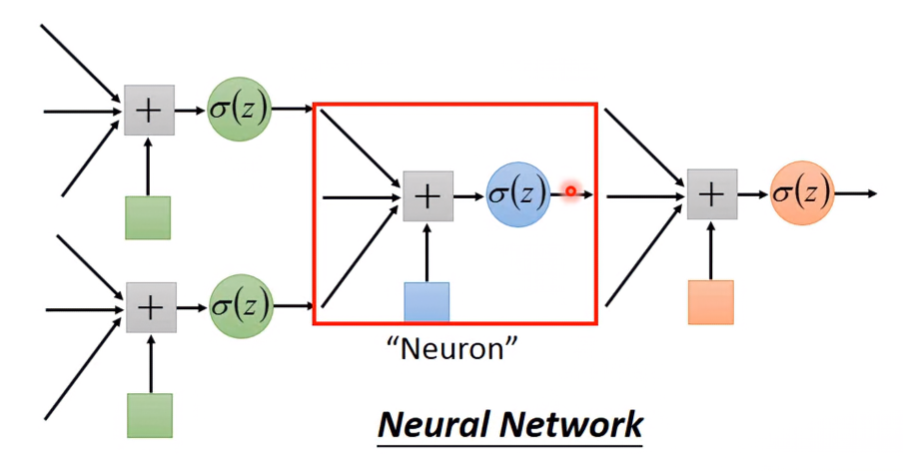
Multi-Level Cascades form a Neural Network
若有多層級的Logistic Regression Cascade,某級Cascade的輸入是上一級Cascade的輸出;輸出是下一級Cascade的輸入。則此級被稱為Neuron,多個Neuron串接在一起,形成的網路被稱為Neural Network