Lecture 6

Lecture 6: Brief Introduction of Deep Learning

Up and downs

1958: Perceptron (linear model)
- 很像Logistic Regression，只是沒有sigmoid的部分
- Frank Rosenblatt在海軍的Project提出的
- 聲稱可以分辨坦克與卡車，就算有樹擋住也能分辨

1969: Perceptron has limitation
- MIT有人出書，就叫「Perceptron」，裡面提到Perceptron因為使用的是線性模型，所以有很多事情都辦不到
- 後人把卡車跟坦克的data重新審視，結果發現兩類照片是在不同天拍攝的，一天是晴天、一天是陰天。所以Perceptron只能分辨亮度，而不是直接認識卡車跟坦克。

1980s: Multi-layer perceptron
- 多層perceptron串接
- 當時的技術跟現今的DNN幾乎無差別
- 有人稱為 Neural Network

1986: Backpropagation
- Geoffrey Hinton 的「Learning representations by bavk-propagating errors」
- 通常對於超過3個隱藏層的神經網路沒有太大幫助

1989: 1 hidden layer is “good enough”, why deep?
- 有人聲稱只要一個隱藏層就能建模任何可能的函數

2006: RBM initialization (breakthrough)
- Geoffrey Hinton 的「A Practical Guide to Training Restricted Boltzmann Machines」
- 如果使用RBM找Fradiewnt Descent的初始值，則學習方式被稱為Deep Lerning；反之，則為Multi-layer Pertron
- 是Graphical Model，而非Neural-based

2009: GPU
- GPU的出現，使得訓練比使用CPU來的快許多

2011: Start to be popular in speech recognition
- 當時人們發現深度學習在語音辨識的成效上十分顯著

2012: win ILSVRC image competition

Three Steps

Deep Learning跟求邏輯回歸一樣，無非是這三大步驟：

以下章節詳細介紹每個步驟。

Step 1: define a set of function

首先要定義函數集，而每一個函數其實就是Neural Network。

Neural Network

在上一篇筆記提到，神經網路其實就是許多個Logistic Regression串接在一起。而每一級Logistic Regression被稱為Neuron，由多個Neuron串接的網路被稱為Neural Network；在網路裡所有neurons的權重與偏移量被稱為 Network paramter $\theta$ 。

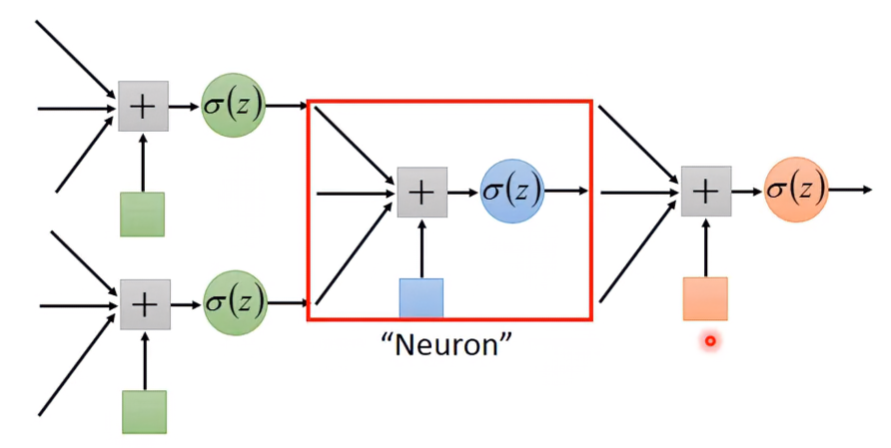
那在網路裡的Neurons是怎麼接起來的？其拓樸長什麼樣子呢？這其實是要自己設計的，不同的連接方式會有不同的網路拓樸結構，以下介紹一個最常見的連接方式。

Fully Connect Feedforward Network

其拓樸結構如下圖，每個neuron都有自己的權重和偏移量，輸入和輸出資料都是向量。從輸入端看進去，這其實就是一個function，不同的 Network parameter 就會有不同的function，這些function就會形成一個function set。

上圖的Network可以以下圖表示，每一級都被稱為layer，每個layer的園點都是一個neuron。Input因為沒有運算所以其實不算一個layer，但還是習慣稱作Input Layer。而中間 Layer 1~Layer L-1被稱為Hidden Layer，Output的前一層Layer L被稱為Output Layer。

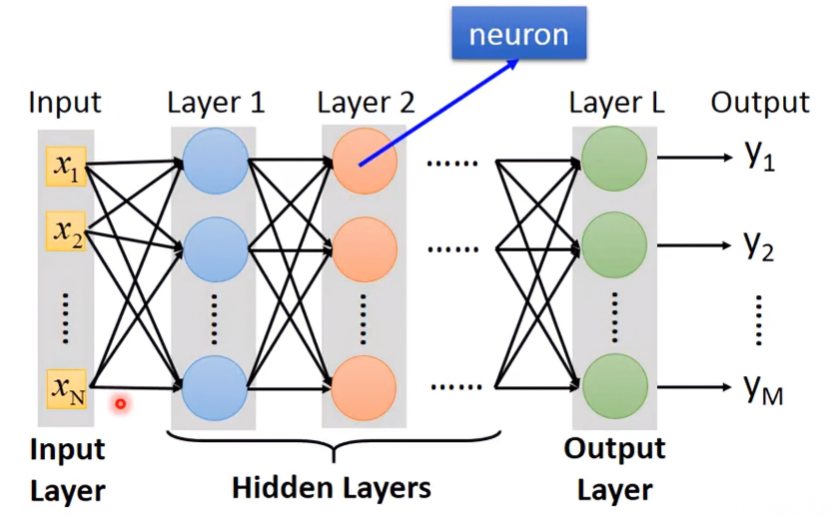
What does “Deep” means?

Deep Learning所謂的Deep指的是神經網路有很多層Hidden Layers，但具體數量要多少呢？其實沒有明確的定義，所以基本上只要是neural network base的方法，都可以被稱為 Deep Learning。

Matrix Operation

神經網路的輸出是輸入向量經由多次與權重以及偏移量矩陣運算得出的結果。

Example - Single Layer Matrix Operation

下圖為某神經網路，計算第一層對第二層的輸出：

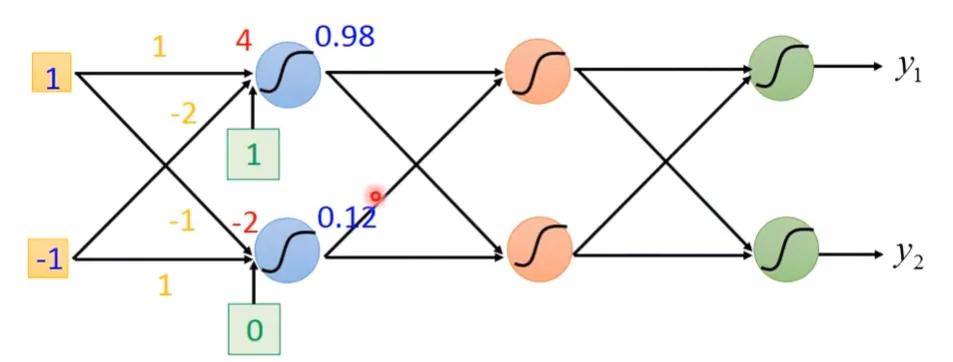
某一個Neuron的權重與偏移量為：

w_1=\begin{bmatrix} 1 & -2 \\ -1 & 1 \end{bmatrix} ,b_1=\begin{bmatrix} 1 \\ 0 \end{bmatrix}

輸入向量為：

x_{in}=\begin{bmatrix} 1 \\ -1 \end{bmatrix}

每一層的特徵轉換公式為：

z_i=w_i\cdot x_i+b_i \\ y_i=\sigma(z_i)

代入公式後，可以得到第一層的輸出：

z_1=\begin{bmatrix} 1 & -2 \\ -1 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ -1 \end{bmatrix} + \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 4 \\ 2 \end{bmatrix}

y_1=\sigma(\begin{bmatrix} 4 \\ 2 \end{bmatrix}) = \begin{bmatrix} 0.98 \\ 0.12 \end{bmatrix}

Multi-Layer Matrix Operation

下圖為某神經網路，可以看到某一層layer都有其專屬的權重與偏移量：

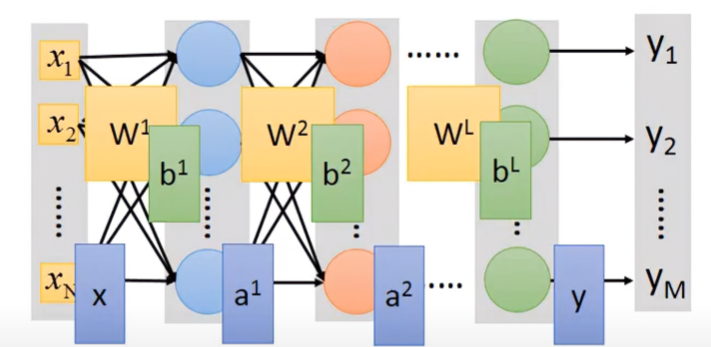
每層的權重與偏移量、輸入輸出皆為矩陣，此神經網路最後的輸出為：

y=f(x)=\sigma(W^L\cdot......\cdot\sigma(W^2\cdot\sigma(W^1\cdot x+b^1)+b^2)+......+b^L)

Speedup of operation with GPU

如果有學過Matrix chain multiplication，會知道多矩陣的運算是很複雜且耗時的，使用CPU運算會需要漫長的等待。使用GPU平行運算，對於時間的消耗有顯著改善。

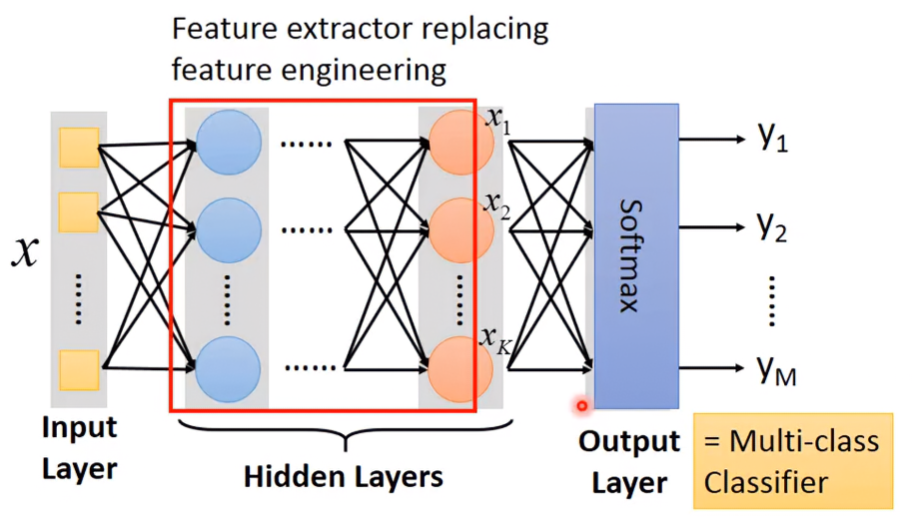
Output Layer

在Output Layer前的部分被稱為Feature extractor，這取代了以前手動作feature engineering。Output Layer是多類別的分類器，它使用的不是輸入x的feature，而是在feature extractor的最後一層輸出已經是被萃取過、最優、最能被separable的feature。

因此只要在Output Layer上一層Softmax，就能把feature分類好。

Example - recognition of image of numbers

假設要對某個大小為16*16的數字圖像做影像辨識：

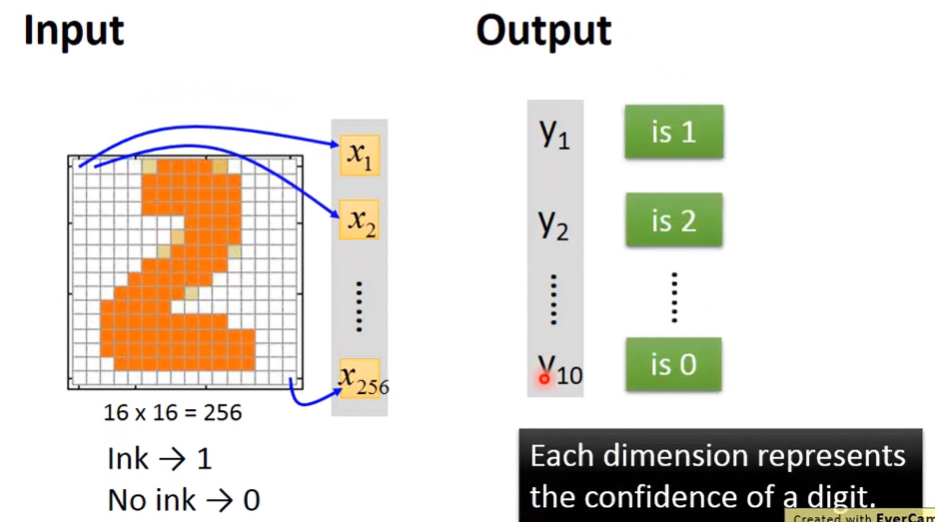
輸入為256個維度的列向量，每個維度對應到圖像上的一個區塊，若區塊是白色，則值為0；若區塊是黑色，則值為1。

x=\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_{256} \end{bmatrix} where\space x_i= \left\{ \begin{array}{c} 1 ,& Ink \space\space\space\space\space\space\\ 0 ,& No\space Ink \end{array} \right.

輸出為10個維度的列向量，每個維度 $x_i$ 代表圖像為數字 $i$ 的機率。假設維度 $x_j$ 的機率是所有維度中最大的，那此圖像最有可能是數字 $j$ ：

y=\begin{bmatrix} y_0 \\ y_1 \\ \vdots \\ y_9 \end{bmatrix} where \space y_i=P(C_i|x)

Solve the example

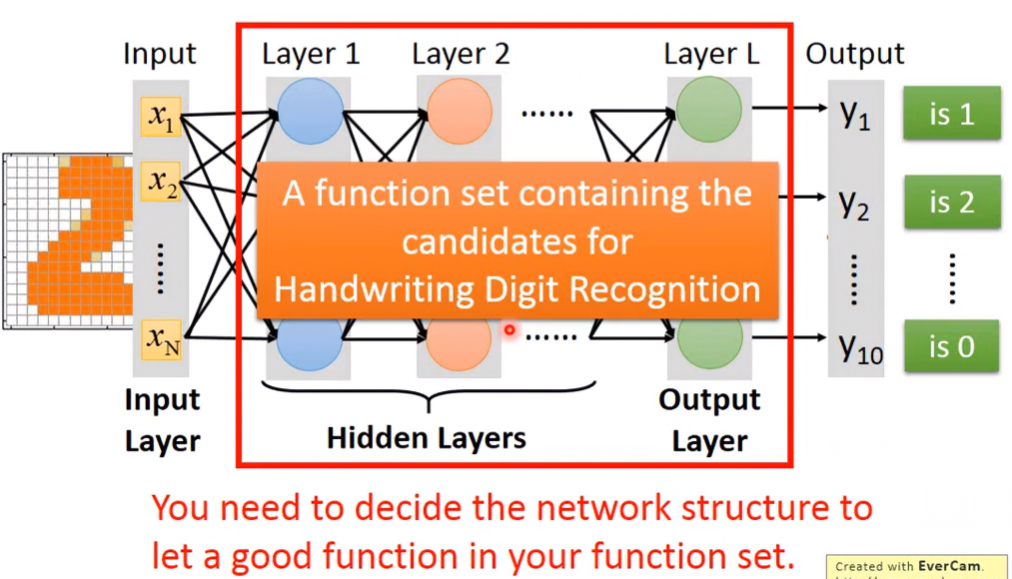
所以現在function的constraints就是輸入要是256維、輸出要是10維的向量，至於中間的Hidden Layers要有幾層、每一層layer要有幾個neuron，這些形成的拓樸結構是要自己設計的，而且function set的設計對於輸出的好壞是很關鍵的。

FAQ

How many layers? How many neurons for each layer?

這是沒有一定答案的，只能憑經驗、直覺和多方的嘗試，去找較佳的 network structure。所以從非deep learning轉成deep learning不一定比較簡單，只是將一個問題轉化成另一個問題。

以往要得到好的結果，要做feature engineering、Feature Transformation，然後找一組好的feature。現在如果換成用deep learning，只是換成要做 network structure 的 design 而已。在某些領域比較適合deep learning，有些就不適合，所以這就case by case。

如果是做語音辨識或影像辨識的話，使用deep learning會比較適合，因為人對於看、聽太淺意識了，我們無法精確知道我們人體到底是怎麼做影像跟語音辨識的。因此，如果是用feature engineering，會在feature要怎麼調這件事上，比較難決定。不如直接設計一個 network structure，讓機器自己去學調整參數，反而比較容易。

但在NLP領域，使用feature engineering可能會比deep learning的效果來的顯著。