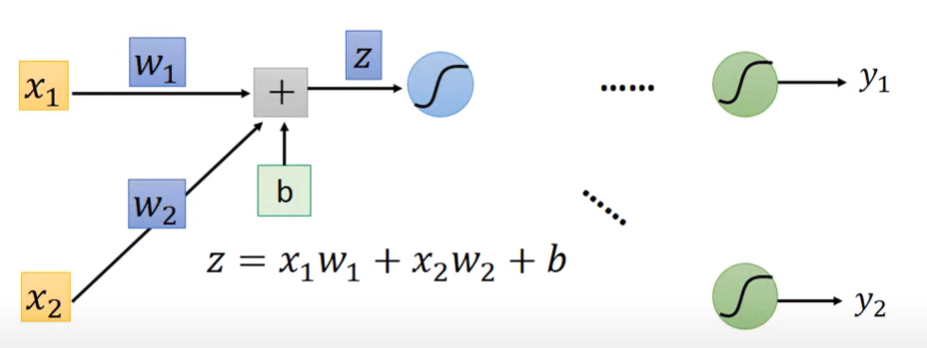Lecture 7

Lecture 7: Backpropagation

Gradient Descent

Backpropagation其實就是Gradient Descent的一種演算法，為甚麼要使用Backpropagation呢？先複習一下平常優化loss的步驟。

Review

假設某個神經網路的network parameters θ\theta為：

θ={w1,w2,...,b1,b2,...}\theta=\{w_1,w_2,...,b_1,b_2,...\}

Loss function對 θ\theta 求梯度：

∇L(θ)=[∂L(θ)∂w1∂L(θ)∂w2⋮∂L(θ)∂b1∂L(θ)∂b2⋮]\nabla L(\theta)=\begin{bmatrix} \frac{\partial L(\theta)}{\partial w_1} \\ \frac{\partial L(\theta)}{\partial w_2} \\ \vdots \\ \frac{\partial L(\theta)}{\partial b_1} \\ \frac{\partial L(\theta)}{\partial b_2} \\ \vdots \end{bmatrix}

Difficulty

如果model比較複雜，像是語音辨識系統，其network parameter的維度可能是百萬級別的。如果要像上面一個一個算總Loss對權重的偏導數的話，會超級耗費時間！所以使用Backpropagation演算法可以有效減少運算的時間複雜度。

Chain Rule

Single parameter function

設有兩函數g、h，g為x的函數，且y為g的函數值；h為y的函數，且z為h的函數值：

y=g(x);z=h(y)y=g(x);z=h(y)

所以當x有變化時，y也會有變化；y有變化時，z也會有變化：

Δx→Δy→Δz\Delta x\rightarrow \Delta y\rightarrow \Delta z

因此z對x的微分需使用連鎖律求解：

dzdx=dzdydydx\frac{dz}{dx}= \frac{dz}{dy} \frac{dy}{dx}

Double parameters function

設有兩函數g、h皆為s的函數，x為g的函數值，y為h的函數值。有一雙變數函數k，其參數有x、y，z為k的函數值：

x=g(s);y=h(s);z=k(x,y)x=g(s);y=h(s);z=k(x,y)

所以當s有變化時，x、y都會有變化；x、y有變化時，z也會有變化：

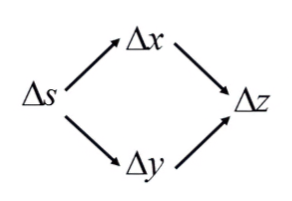
因為z受到兩個變數的變化而變化，且兩個變數為獨立，所以可以寫成全微分的形式：

dzds=∂z∂xdxds+∂z∂ydyds\frac{dz}{ds}= \frac{\partial z}{\partial x} \frac{dx}{ds} + \frac{\partial z}{\partial y} \frac{dy}{ds}

Backpropagation

Network Structure

整個求Loss function的流程如下：

假設神經網路架構如下：

先從第一層的第一個Neuron來看：

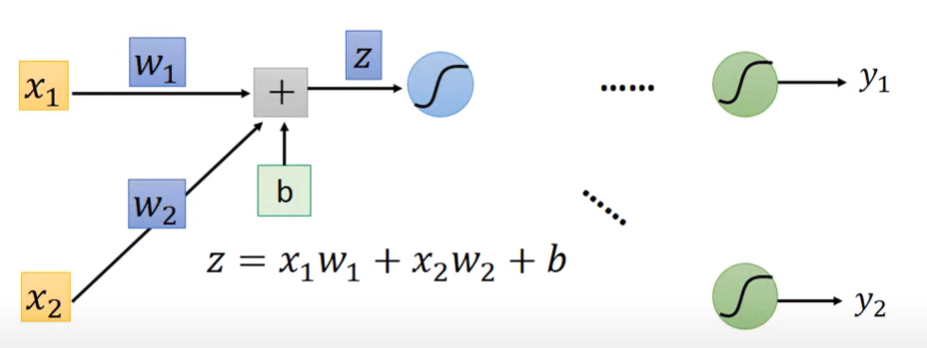
Partial Derivative on Loss function

先求Total Loss function，再求它對權重的偏導：

L(θ)=∑n=1NCn(θ)⇒∂L(θ)∂w=∑n=1N∂Cn(θ)∂wL(\theta)=\sum_{n=1}^NC^n(\theta) \Rightarrow \frac{\partial L(\theta)}{\partial w} = \sum_{n=1}^N \frac{\partial C^n(\theta)}{\partial w}

右式Cost function對權重的偏導可以單獨提出來，從求整體Loss變成求單筆資料的Loss。根據chain rule可以得出：

∂C∂w=∂C∂z∂z∂w\frac{\partial C}{\partial w}= \frac{\partial C}{\partial z} \frac{\partial z}{\partial w}

對於右式兩項偏導數，有其名稱與意義：

Forward pass

Derivation

對於某一級Neuron，其輸入為 x1,x2x_1,x_2 ，權重分別為 w1,w2w_1,w_2，偏移量為 b，則其對activation function的輸入值z為：

z=w1x1+w2x2+bz=w_1x_1+w_2x_2+b

則forward pass的結果為：

∂z∂w1=x1，∂z∂w2=x2\frac{\partial z}{\partial w_1}=x_1 ， \frac{\partial z}{\partial w_2}=x_2

可以發現z對權重求導的結果，是連接該權重的輸入值。

Example

對於所有參數算出 ∂z∂w\frac{\partial z}{\partial w}：

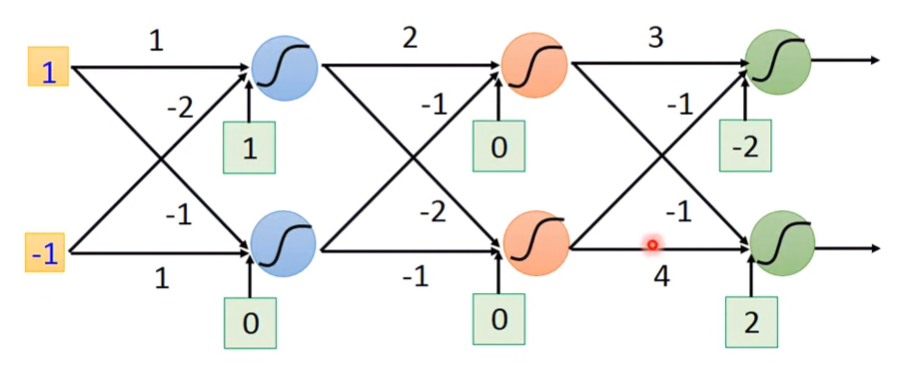
其值就是連接該權重的輸入值：

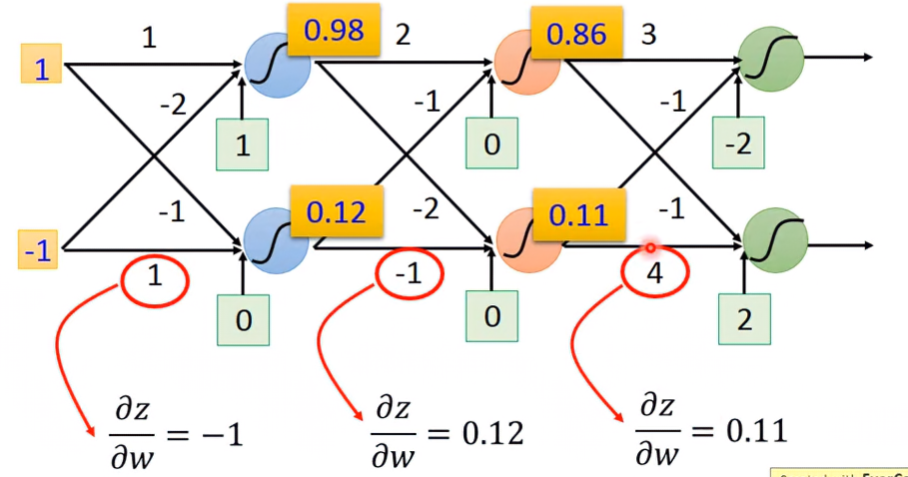
Backward pass

Derivation

先取某一級neuron的activation function：

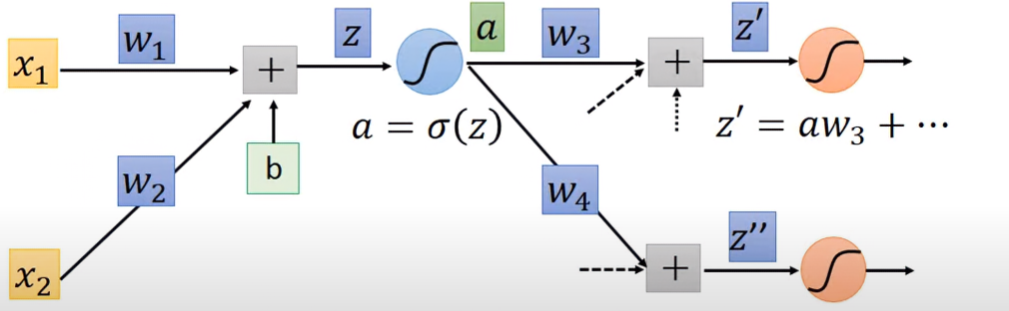
設a為z經過sigmoid後的結果 a=σ(z)a=\sigma{(z)}。將z的變化，從z傳導到a，以此算出 ∂C∂z\frac{\partial C}{\partial z}：

∂C∂z=∂C∂a∂a∂z\frac{\partial{C}}{\partial{z}} = \frac{\partial{C}}{\partial{a}} \frac{\partial{a}}{\partial{z}}

後項a對z的偏導比較好算：

∂a∂z=∂σ(z)∂z=σ(z)⋅(1−σ(z))=σ′(z)\frac{\partial{a}}{\partial{z}} = \frac{\partial{\sigma{(z)}}}{\partial{z}} = \sigma{(z)}\cdot(1-\sigma{(z)}) =\sigma'{(z)}

因為z已經確定了，所以可以被視為常數，因此 ∂a∂z\frac{\partial{a}}{\partial{z}} 也可被視為常數。

前項C對a的偏導比較難算，因為不會知道最後的C對目前a的關係到底長怎樣，如果要繼續向下一級推導的話，會長這樣：

∂C∂a=∂C∂z′∂z′∂a+∂C∂z′′∂z′′∂a=w3∂z′∂a+w4∂z′′∂a\frac{\partial{C}}{\partial{a}} = \frac{\partial{C}}{\partial{z'}} \frac{\partial{z'}}{\partial{a}} + \frac{\partial{C}}{\partial{z''}} \frac{\partial{z''}}{\partial{a}} = w_3\frac{\partial{z'}}{\partial{a}} + w_4\frac{\partial{z''}}{\partial{a}}

因為a的的下一級有兩個neurons，就很像tree的父節點有兩個子節點，a的變化會產生z’與z’’的變化。因此C對a的求導，須以全微分表示。

整合至 ∂C∂z\frac{\partial{C}}{\partial{z}}：

∂C∂z=σ′(z)[w3∂C∂z′+w4∂C∂z′′]\frac{\partial{C}}{\partial{z}}=\sigma'{(z)} [ w_3\frac{\partial{C}}{\partial{z'}} + w_4\frac{\partial{C}}{\partial{z''}} ]

從上述結果可以發現，這級的偏導依賴下級偏導的結果，下級偏導的結果也會依賴下下級偏導的結果。這樣周而復始，直到遇到output layer，才能把最後的結果從後面代回前面。那為什麼不一開始就從最後面算就好？

Meaning of “Backward”

沒錯，就是要從最後算回前面，所以才叫做 “Backward pass”！

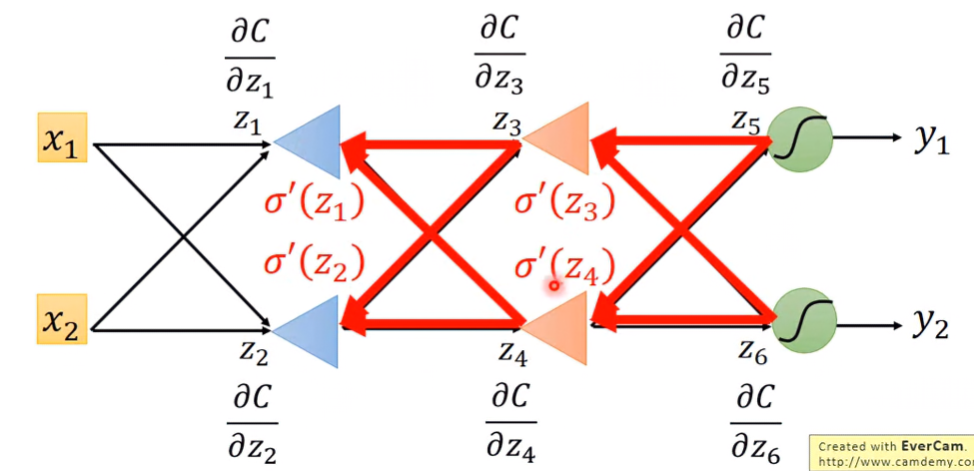
可以想像有一個新的network，其輸出與輸入順序與原本的相反。在這新的network求backward pass，從前面開始算到後面，才不會遇到上面「Derivation」章節算到最後的窘境。

Output Layer通常是一層softmax，因為其輸出y跟Cost function有直接關係，所以可以輕易求得 ∂C(y,y^)∂y\frac{\partial{C(y,\hat{y})}} {\partial y}。而它的輸入 z5z_5 對Cost function的偏導與 ∂C(y,y^)∂y\frac{\partial{C(y,\hat{y})}} {\partial y} 有關係，所以就會很好算，如此周而復始，一直算到最前面：

∂C(y,y^)∂y→∂C∂zn&∂C∂zn−1→⋯→∂C∂z2&∂C∂z1\frac{\partial{C(y,\hat{y})}} {\partial y} \rightarrow \frac{\partial{C}} {\partial z_{n}} \& \frac{\partial{C}} {\partial z_{n-1}} \rightarrow \dots \rightarrow \frac{\partial{C}} {\partial z_{2}} \& \frac{\partial{C}} {\partial z_{1}}

Summary

最後求出了 Forward Pass ∂z∂w\frac{\partial z}{\partial w} 與 Backward Pass ∂C∂z\frac{\partial C}{\partial z} 之後，就可以得到Cost function對某權重的偏導到底是多少了，最後就可以重複迭代直到找到最佳解：

wi+1←wi−η∂C∂wiw_{i+1}\leftarrow w_i-\eta\frac{\partial C}{\partial w_i}