Lecture 9: Tips for Training DNN

Recipe of Deep Learning

以下是Train DNN的過程。當Testing Data的結果沒那麼好時，這現象被稱為Overfitting，但要注意的是，這是在Training Data表現很好的前提下成立；如果Training Data的表現就不好，那就不是Overfitting，只是單純沒訓練好而已。

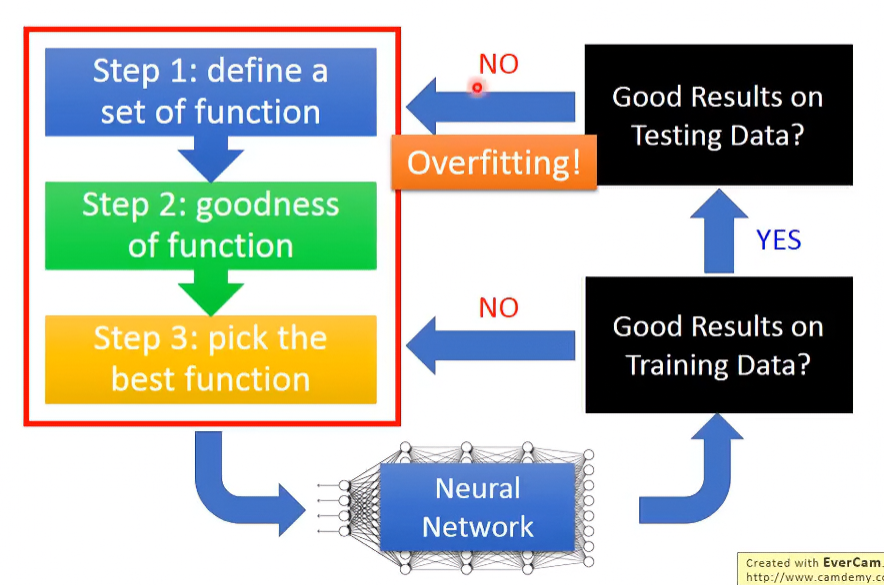
以下把在Training Data以及Testing Data表現不好的情況分開討論，各情況的應對方式如下圖：

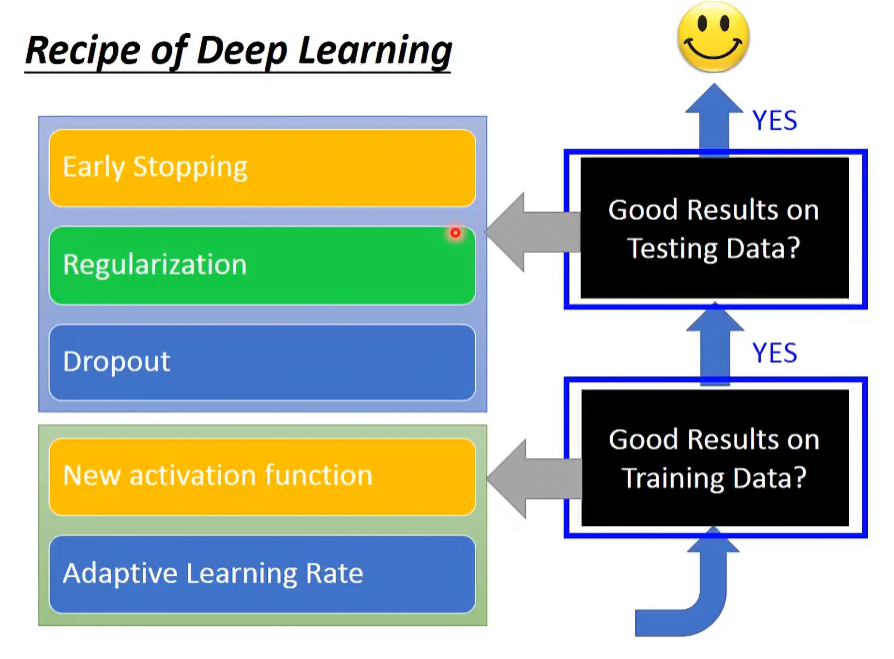
在Training Data表現不好的成效時，有兩種方式解決：

在Testing Data表現不好且Training Data表現很好的成效時，有三種方式可以解決：

New activation function

在過去年代，比較常用的activation function是sigmoid function，可以看到下圖，當layer越來越多時，正確率會大幅下降：

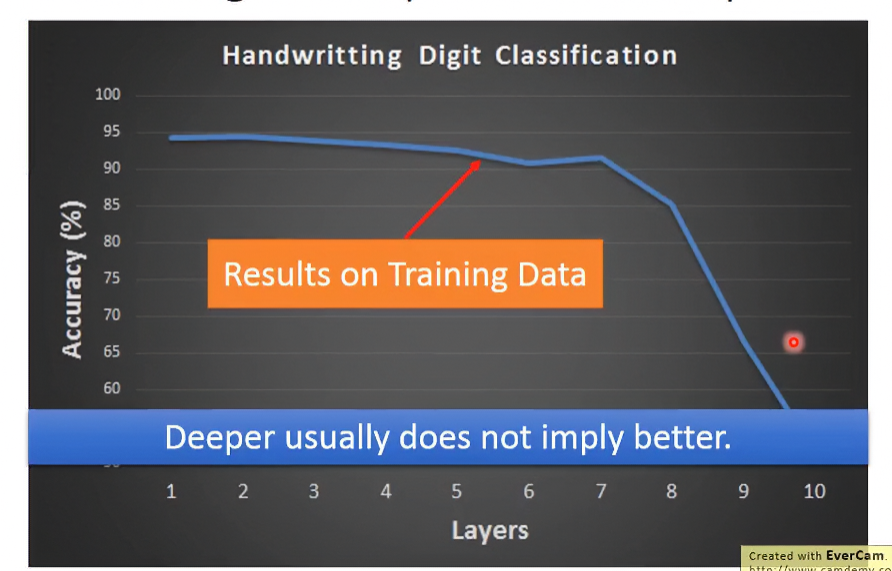
這個現象叫做Vanishing Gradient Problem，詳細介紹如下。

Vanishing Gradient Problem

以下是Sigmoid function圖形，可以看到其輸入對輸出的變化影響小：

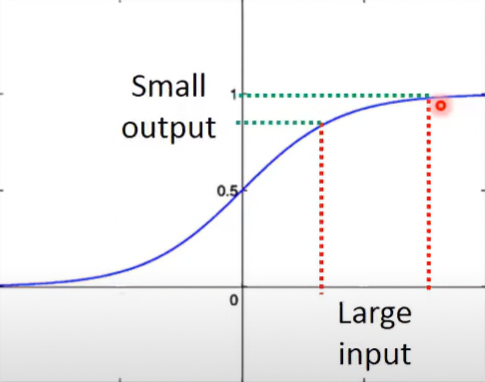
所以當我們在求Gradient Descent時，等於是在求權重對Loss function的變化 ∂C∂w\frac{\partial C}{\partial w}。如果layer越多，那麼在第一層Hidden layer的權重變化 Δw\Delta w，會經過多次的Sigmoid，導致其傳導的變化越來越小。到最後一層時， Δw\Delta w 對 ΔC\Delta C 就變超級小，幾乎無影響。

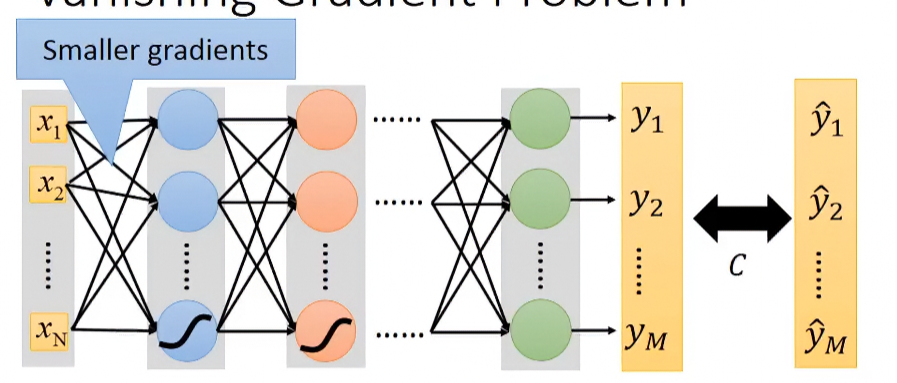
解決方式就是替換avtivation function，以下介紹幾個效果不錯的function。

ReLU

全名為 Rectified Linear Unit，為現在比較常用的 activation function 之一。假設其輸入為x，輸出為a，則其函數定義：

a=f(z)={z,z≥00,z<0a=f(z)=\left\{ \begin{array}{c} z ,& z\geq 0 \\ 0 ,& z\lt0 \end{array} \right.

其圖形：

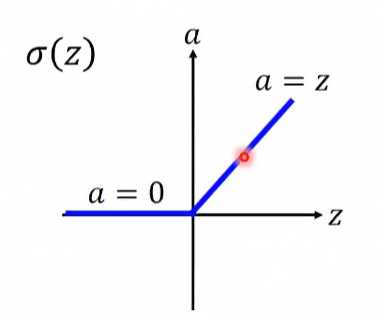
使用ReLU的原因：

Model Structure

假設原本NN的架構長這樣：

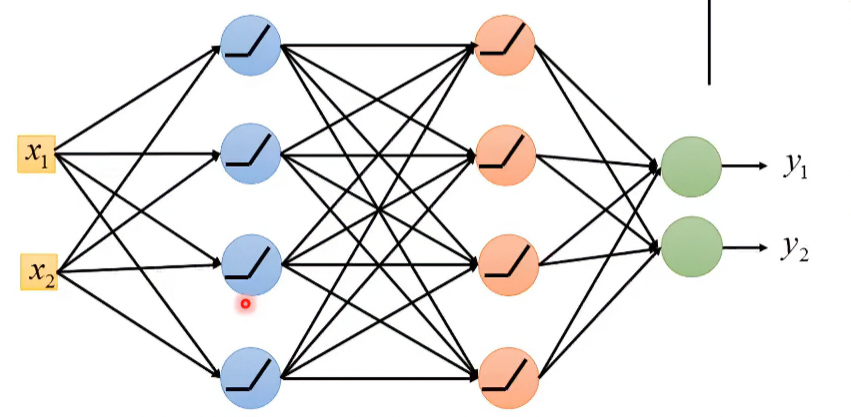
如果考慮輸入的話，其model可以變得更瘦小、輕便：

Doesn’t it affect the efficiency?

因為ReLU的特性就是在輸入值大於等於0時，輸出等於輸入，所以在輸入變化小時，整體model是線性的。但當輸入變化大時，因為operation region的改變，所以整體model還是被視為non-linear model，其可靠性還是有的。

Is it differential?

雖然在 a=0 那點不可微，但是其他地方是可微的，所以在實作上會忽略 a=0 那點的微分值，或另那點的微分值隨便一個數值。

ReLU - variant

使用ReLU在input小於0時，其導數為0，這時候無法更新參數。為解決這問題，可以在input小於0的地方，讓他導數不為0。

Leaky ReLU

例如Leaky ReLU就在input等於0時，令輸出a=0.01z，其函數定義如下：

a=f(z)={z,z≥00.01z,z<0a=f(z)=\left\{ \begin{array}{c} z ,& z\geq 0 \\ 0.01z ,& z\lt 0 \end{array} \right.

圖形如下：

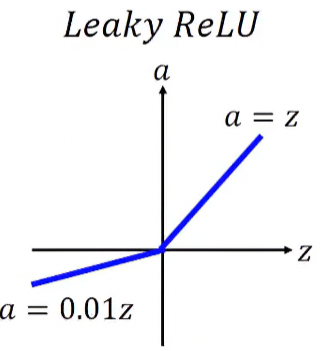
Parametric ReLU

那可以不要是0.01z嗎？當然可以！

像是Parametric在input小於0時，其輸出為一常數倍的z，此常數在不同neuron可能不一樣，是可以在Gradient descent時被學出來的：

a=f(z)={z,z≥0αz,z<0a=f(z)=\left\{ \begin{array}{c} z ,& z \geq 0 \\ \alpha z ,& z \lt 0 \end{array} \right.

其圖形如下：

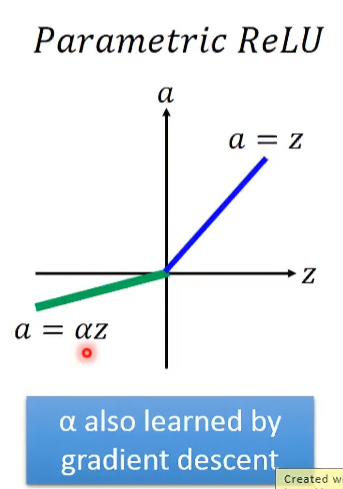
那其實也不一定要是ReLU的樣子，以下介紹一實用activation function。

Maxout

輸入值經過加權、偏移後，把這些值group起來，每個group再挑最大值。

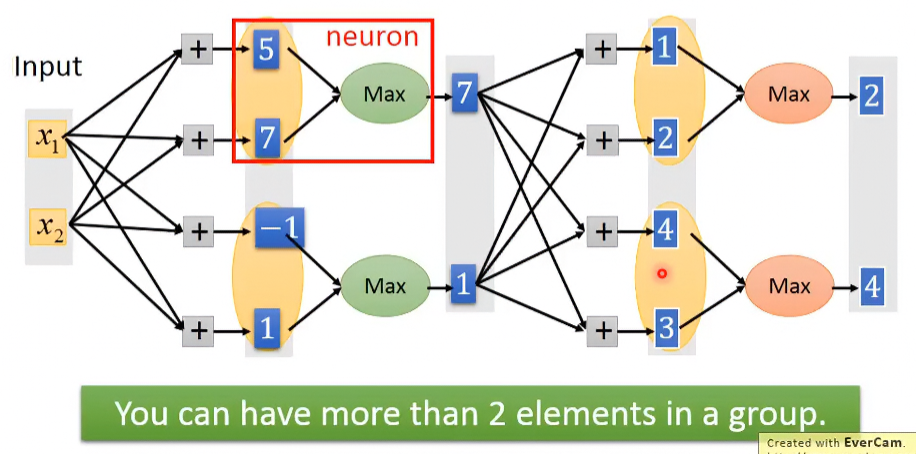
至於那些一個group幾個值？那些值要形成group？這問題跟network structure一樣要自己設計。

Make ReLU by Maxout

ReLU其實是Maxout的一個special case，只要結構如下，就能用maxout模擬ReLU。首先假設輸入值為： [x1]\begin{bmatrix} x \\1 \end{bmatrix}，第一組參數為： [wb]\begin{bmatrix} w \\ b \end{bmatrix}，第二組參數為： [00]\begin{bmatrix} 0 \\ 0 \end{bmatrix}，則兩組方程值與max函數的輸出a為：

z1=w⋅x+b，z2=0a=max⁡{z1,z2}z_1=w\cdot x+b ， z_2=0 \\ a = \max{\{z_1, z_2\}}

其圖形為：

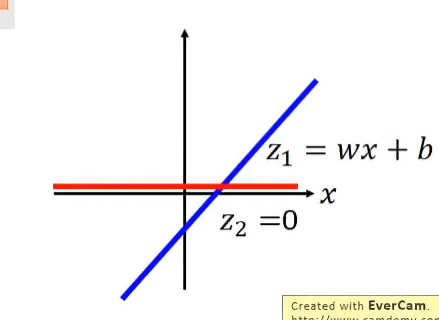
如果不考慮b的話，可以發現輸出a確實為ReLU：

a=max{z1,z2}={z,z≥00,z<0a=max\{z_1,z_2\}= \left\{ \begin{array}{c} z ,& z\geq0 \\ 0 ,& z\lt 0 \end{array} \right.

Learnable Actvation Function

假設第二組參數為 [w′b′]\begin{bmatrix} w' \\ b' \end{bmatrix}，則兩方程式為：

z1=w⋅x+b；z2=w′⋅x+b′z_1=w\cdot x+b；z_2=w'\cdot x+b'

maxout的輸出結果就是兩方程式的疊加：

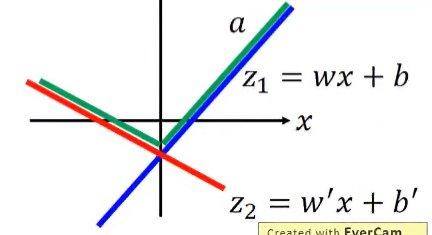
因為activation function跟權重有關，所以在訓練模型時，activation function也在自適應學習。

Training problem of Maxout

你可能會問，maxout用了max函數，這樣要怎麼微分？但這其實不是什麼太大的問題。

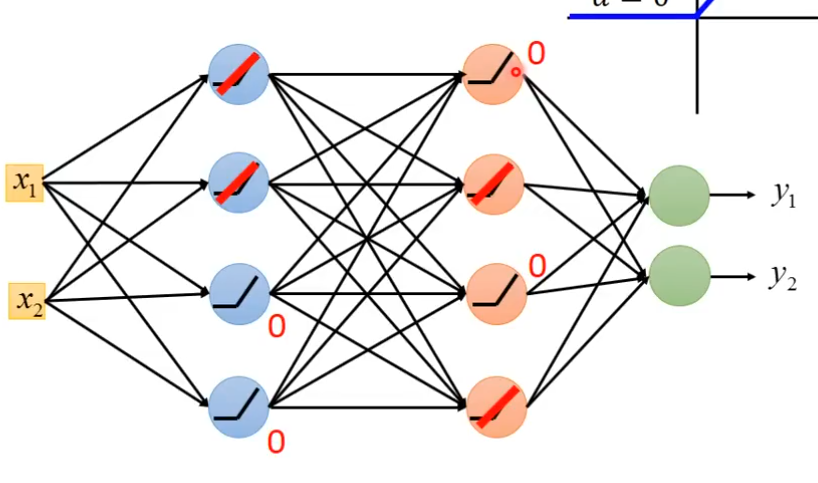
假設有個NN如下圖：

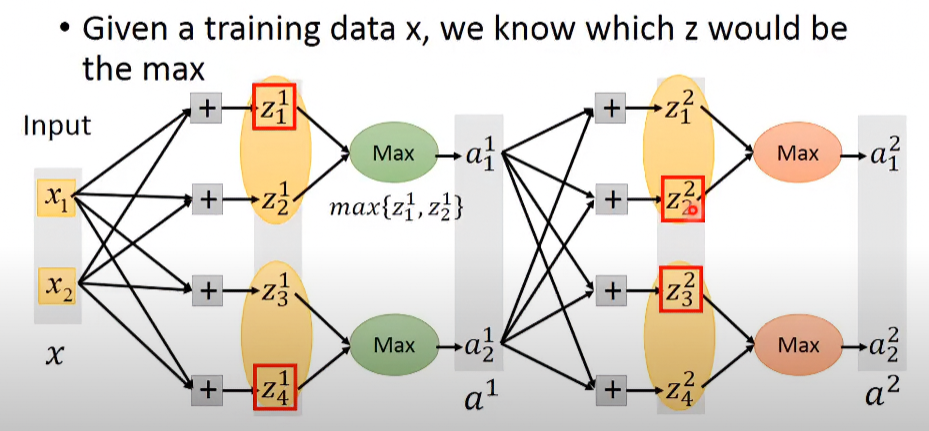
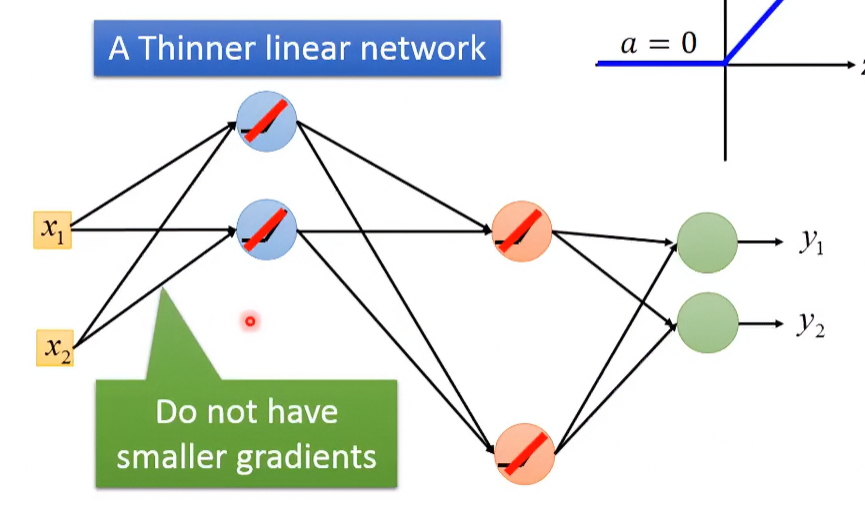
在某個input data的輸入下，其model被縮略至下圖：

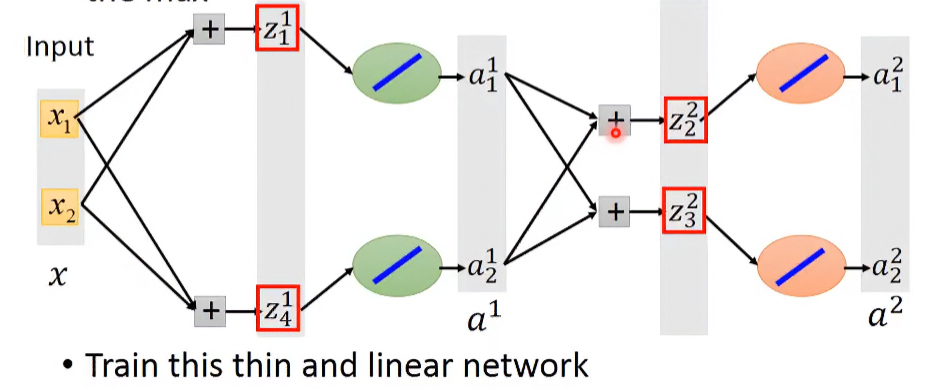
可以看到這其實就是一般的linear model，所以把它當成一般的線性模型，對線性方程式微分就好。

到這你可能又會問，那這樣被省略的權重不就不會被訓練到了嗎？但其實每次輸入值的不同，都會訓練到不同組的權重，所以當訓練資料夠多時，就不會有權重沒被訓練到的問題。

Adaptive Learning Rate

Review - Adagrad

當多變數函數在多個不同方向的切片，有不同弧度時，使用adagrad可以避免高估偏導數：

wt+1←wt−η∑i=0t(gi)2gtw^{t+1}\leftarrow w^t-\frac{\eta}{\sqrt{\sum^t_{i=0}(g^i)^2}}g^t

但是之前給的例子比較簡單，在實際應用上可能會遇到，就算在某方向的切片上，其learning rate的變化率還是很陡峭：

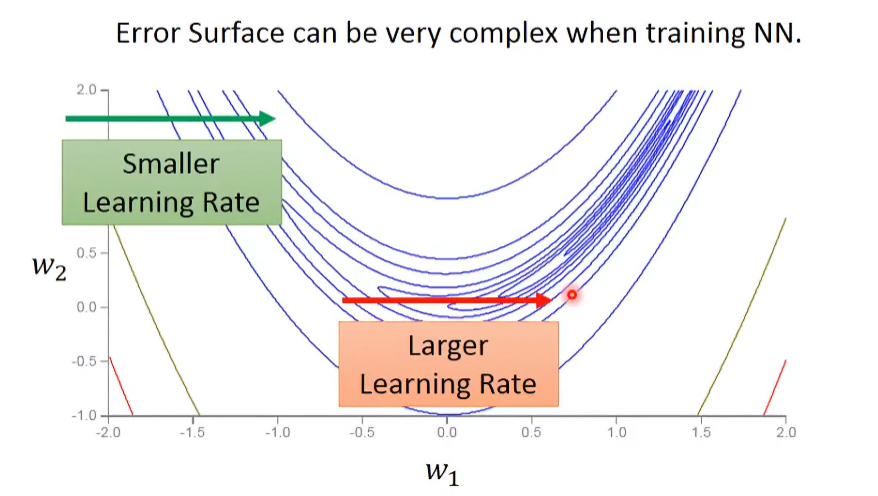
所以需要動態的調整learning rate，有一個比adagrad更進階的方法，叫做RMSProp。

RMSProp

迭代時，其目前的root mean square跟過往的參數有關，迭代過程如下：

w1←w0−ησ0g0；σ0=g0w2←w1−ησ1g1；σ1=α(σ0)2+(1−α)(g1)2w3←w2−ησ2g2；σ2=α(σ1)2+(1−α)(g2)2⋮wt+1←wt−ησtgt；σt=α(σt−1)2+(1−α)(gt)2w^1\leftarrow w^0 - \frac{\eta}{\sigma^0}g^0；\sigma^0=g^0 \\ w^2\leftarrow w^1 - \frac{\eta}{\sigma^1}g^1；\sigma^1=\sqrt{\alpha(\sigma^0)^2+(1-\alpha)(g^1)^2} \\ w^3\leftarrow w^2 - \frac{\eta}{\sigma^2}g^2；\sigma^2=\sqrt{\alpha(\sigma^1)^2+(1-\alpha)(g^2)^2} \\ \vdots \\ w^{t+1}\leftarrow w^t - \frac{\eta}{\sigma^t}g^t；\sigma^t=\sqrt{\alpha(\sigma^{t-1})^2+(1-\alpha)(g^t)^2}

Local Minimum Problem

我們都擔心訓練時的圖形分部長這樣，因為會更新點會卡在local minimum裡：

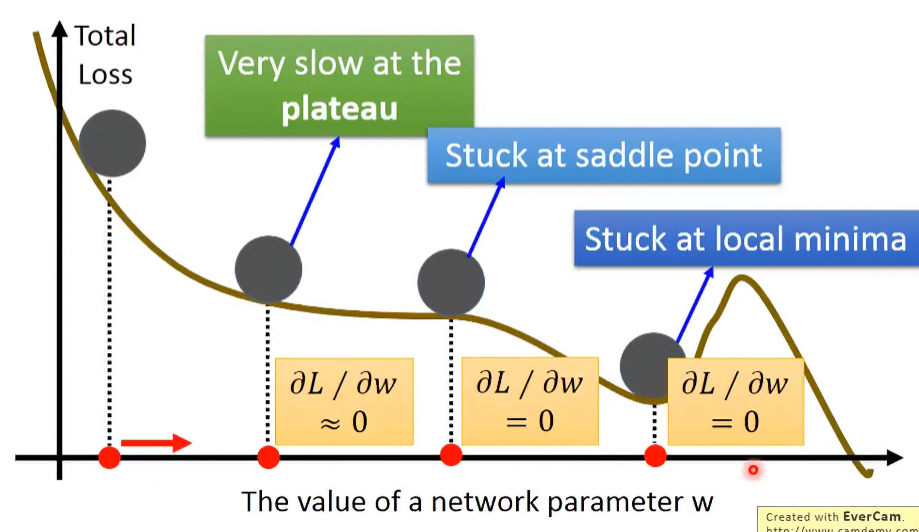
但其實Yann LeCun說過不用太擔心，因為其實在error surface上是沒有太多local minumum的。因為要有一個local minimum，則每個dimension的圖形都必須跟上圖一樣有個相對但非絕對的低點。假設每個dimentsion有local minimum的機率為 pp，那因為在真實的模型，其參數量龐大，如果每個dimension都要有local minimum的話，其機率會非常小：

lim⁡n→∞pn=0 where 0<p<1\lim_{n\rightarrow\infin}p^n=0 \space where \space 0\lt p \lt1

所以當覺得更新點走一走遇到低窪的時候，其實有很大的機率已經走進global minimum裡了。

那也有一個heuristic的方法可以解決local minimum跟plateau的問題，也就是靠模擬真實世界的慣性與動量去決策更新點步伐。在介紹此方法前，先回顧一下原本的Gradient Descent。

Review - Vanilla Gradient Descent

令更新的參數為原參數減去學習率與損失函數梯度的乘積，其每次步行方向都與梯度向量相反：

θt+1=θt−η∇g(θt)Stop untill ∇L(θt)≈0\theta^{t+1}=\theta^t-\eta\nabla{g(\theta^t)} \\ Stop\space untill\space \nabla L(\theta^t) \approx0

示範圖形如下：

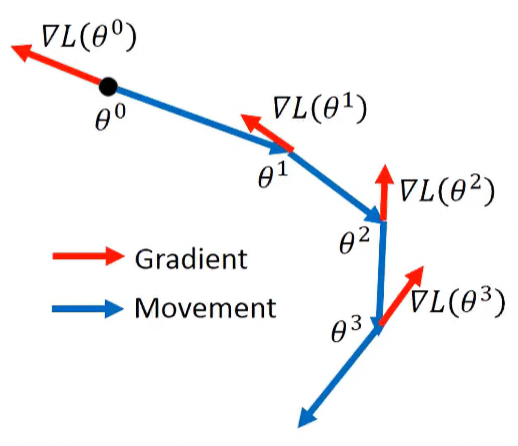
Momentum

若要類比物理世界中的慣性，在此必須先加入移動慣量(類似速度)的概念，新的參數點會與上次移動量有關。在一開始，移動慣量為0，且有初始位置：

v0=0；Start Point θ0v^0=0；Start\space Point \space \theta^0

第一次的迭代：

v1=λv0−η∇L(θ0)v^1=\lambda v^0-\eta \nabla L(\theta^0)
θ1=θ0+v1\theta^1=\theta^0+v^1

第二次的迭代：

v2=λv1−η∇L(θ1)v^2=\lambda v^1-\eta \nabla L(\theta^1)
θ2=θ1+v2\theta^2=\theta^1+v^2

從上面兩次迭代，大概可以看出移動慣量其實是過去所有權重後的梯度總和：

v0=0⇒v1=−η∇L(θ0)⇒v2=−λη∇L(θ0)−η∇L(θ1)v^0=0\Rightarrow v^1=-\eta\nabla L(\theta^0)\Rightarrow v^2=-\lambda\eta\nabla L(\theta^0)-\eta\nabla L(\theta^1)

從下圖可以看到，在遇到local minimum時，就算偏導為0，依然可以借助慣性的力量離開：

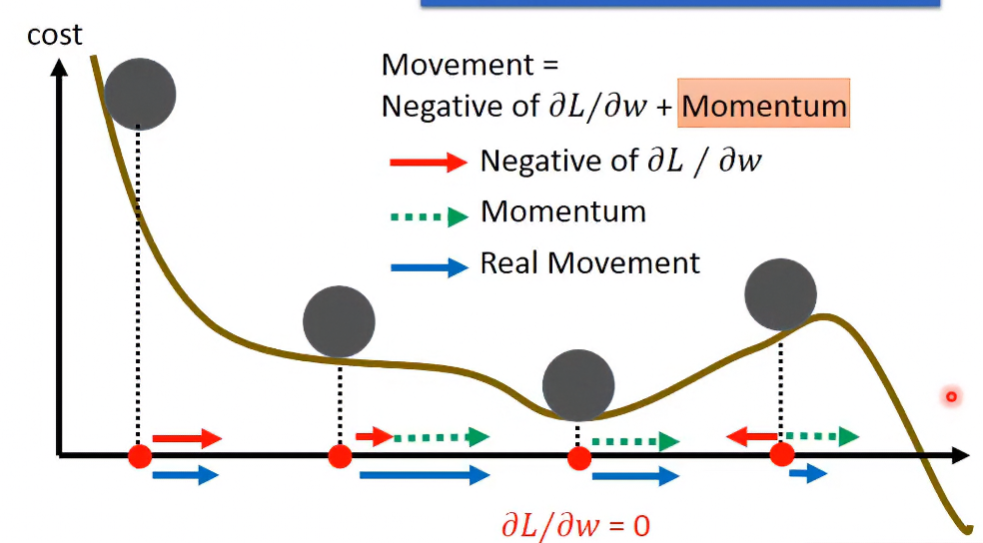
在離開local minimum後的爬坡，若 λ\lambda 足夠的話，是有機會藉慣性越過小峰到global minimum的。

Adam

RMSProp + Momentum 的組合就是 Adam，其演算法如下：

可以看到裡面還有RMSprop跟momentum沒有的步驟，就是把 m^t,v^t\hat{m}_t,\hat{v}_t 除以 1−β1-\beta ，這個叫做bias-corrected，想知道詳細原因的話就去看論文。

Early Stopping

因為bias跟variance的關係，testing data的loss會在training data的loss變小時逐漸變大，所以假設知道所有data對Total Loss的整體關係，那就找testing data的loss最低的那點。

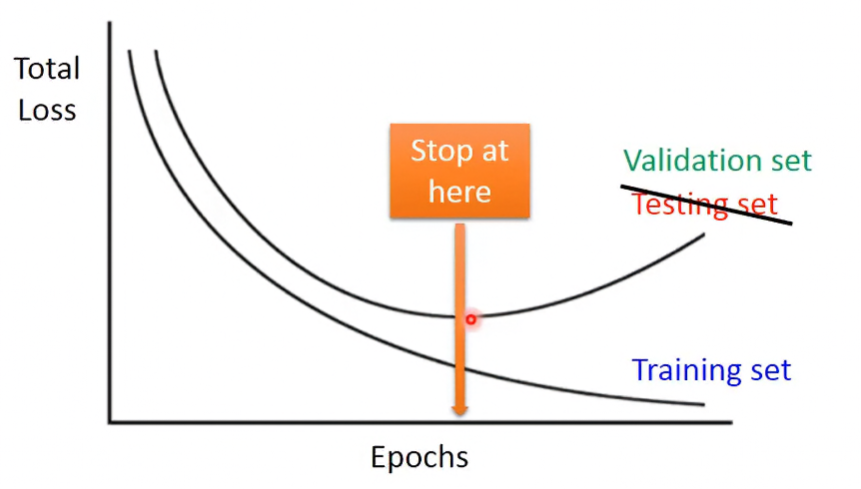
這裡的testing data不是真正意義上的隨機資料，而是自己可以控制的validation data。

Regularization

設定新的Loss function，為原Loss function加上Regularization term。此舉使函數更平滑，讓雜訊的影響減小。

L′(θ)=L(θ)+Regularization termL'(\theta)=L(\theta)+Regularization \space term

我們知道 network parameter θ\theta 其實就是所有權重與偏移量的集合的向量， θ={w1,w2,⋯ ,b1,b2⋯ }\theta = {\{w_1, w_2, \cdots,b_1,b_2\cdots\}}。Regularization term其實就是取 θ\theta 的 norm，可以是L1-norm或L2-norm等等。

如果使用L2-norm的話：

∥θ∥2=(w1)2+(w2)2+⋯\left\lVert\theta\right\rVert_2 = (w_1)^2+(w_2)^2+\cdots
L′(θ)=L(θ)+λ12∥θ∥2⇒∂L′∂w=∂L∂w+λwL'(\theta)=L(\theta)+\lambda\frac{1}{2} \left\lVert\theta\right\rVert_2 \Rightarrow \frac{\partial L'}{\partial w} = \frac{\partial L}{\partial w} + \lambda w
wt+1←wt−η∂L′∂w=wt−η(∂L∂w+λwt)=(1−ηλ)wt−η∂L∂ww^{t+1}\leftarrow w^t-\eta\frac{\partial L'}{\partial w}=w^t-\eta(\frac{\partial L}{\partial w}+\lambda w^t)=(1-\eta\lambda)w^t-\eta\frac{\partial L}{\partial w}

如果使用L1-norm的話：

∥θ∥1=∣w1∣+∣w2∣+⋯\left\lVert\theta\right\rVert_1 = |w_1|+|w_2|+\cdots
L′(θ)=L(θ)+λ12∥θ∥1⇒∂L′∂w=∂L∂w+λsgn(w)L'(\theta)=L(\theta)+\lambda\frac{1}{2} \left\lVert\theta\right\rVert_1 \Rightarrow \frac{\partial L'}{\partial w} = \frac{\partial L}{\partial w} + \lambda sgn(w)
wt+1←wt−η∂L′∂w=wt−η(∂L∂w+λsgn(wt))=wt−η∂L∂w−ηλsgn(wt)w^{t+1}\leftarrow w^t-\eta\frac{\partial L'}{\partial w}=w^t-\eta(\frac{\partial L}{\partial w}+\lambda sgn(w^t))= w^t-\eta\frac{\partial L}{\partial w}-\eta\lambda sgn(w^t)

可以看到使用L2-norm時，每次都會讓 wtw^t 乘以一個接近0.99的數，這個叫做 weight decay。使用L1-norm跟L2-norm之間還是有差異的，像是L1-norm的結果會比較sparse。

Weight Decay

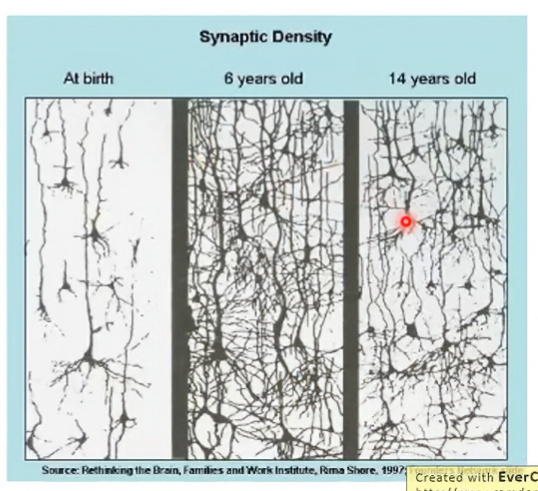
weight decay與人腦神經有異曲同工之妙。當某組weight部會很常被用到時，那那組weight的值很快就會被decay到0。就像人類在14歲時比在6歲時的神經來的少，這是因為在成長的過程中捨棄了不重要的記憶/連結。

Dropout

Dropout顧名思義是要丟棄神經元的意思，有分Training跟Testing兩種。

Training

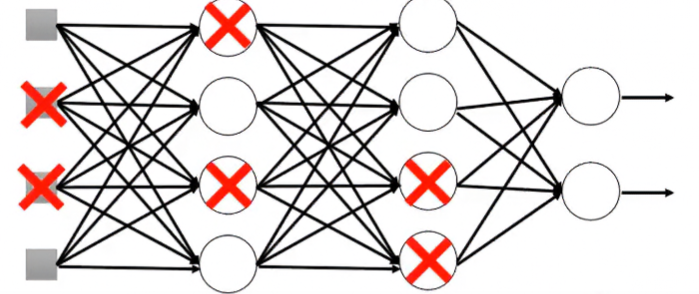
在每次更新參數時，每個neuron都有 p%p\% 的機率會被丟棄。部分neuron被丟棄後的network會變得更瘦小。

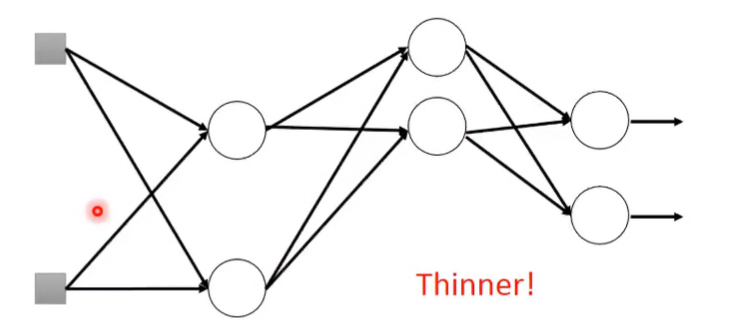
Dropout後的Training正確性會比原本來的差，以換來Testing的正確性提升。

Testing

在testing時不做Dropout。

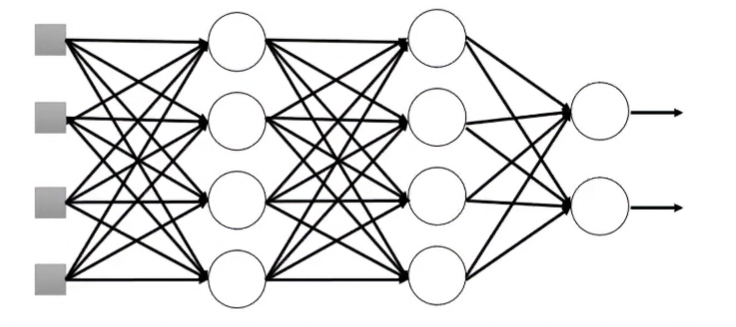
但假設Training時的Dropout rate為 p%p\% ，則Testing時要把所有權重設為原本的 1−p1-p 倍。

Intuitive reason

Dropout的方法看起來很神奇，而且蠻有效的，但從直觀上來看，是有理由可以解釋的。

在Training時Dropout，因為神經網路更細瘦，所以在相同知識量下，其每單位神經乘載的知識量會變大，所以很像在平常訓練時往腳上綁重物；在Testing時，就很像在實際上場時拿下重物，因為平時訓練量很足，所以能比較好應變。

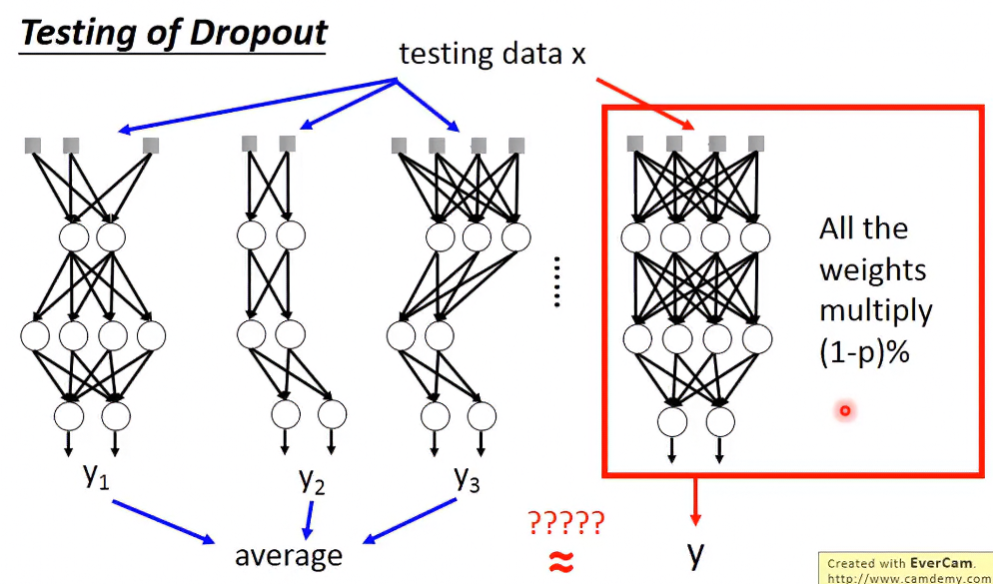
Why multiply 1-p?

在Training時，假設 p=50%p=50\% ，那代表以期望值來看，四條神經會有兩條被丟棄。

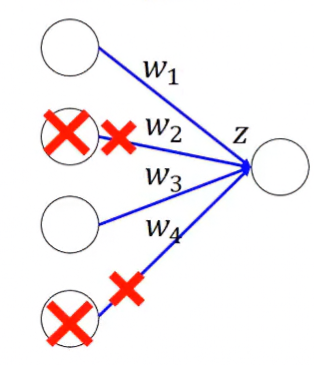
在Testing時，所有神經都會在，代表其輸出值 z′≈2zz'\approx 2z。

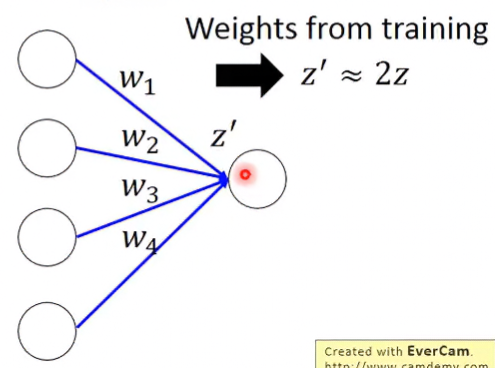
所以要把各權重砍半，得到的 z′z' 才會大約與訓練的相同。

Dropout is a kind of ensemble

Ensemble

複雜的模型往往bias小、variance高，所以若把多個複雜model的結果平均起來的話，可以有效將variance降低。

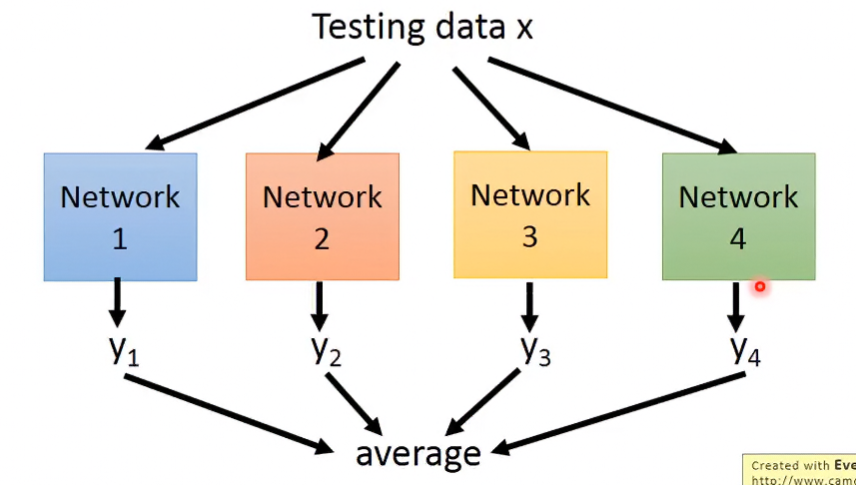
Dropout

Dropout是一種終極的ensemble，為甚麼這麼說呢？假設目前有M個neuron，每個neuron都有 50%50\% 的機率被丟棄，這樣共有 2M2^M 個network的可能性。

在Training時，無法把這麼多可能性的network都訓練過一次所以在訓練時會分好幾個不同stucture的minibatch訓練，並且每個weight都是shared的，每個batch在訓練時都不會把weight丟掉。所以這等同於把所有batch平均的意思。

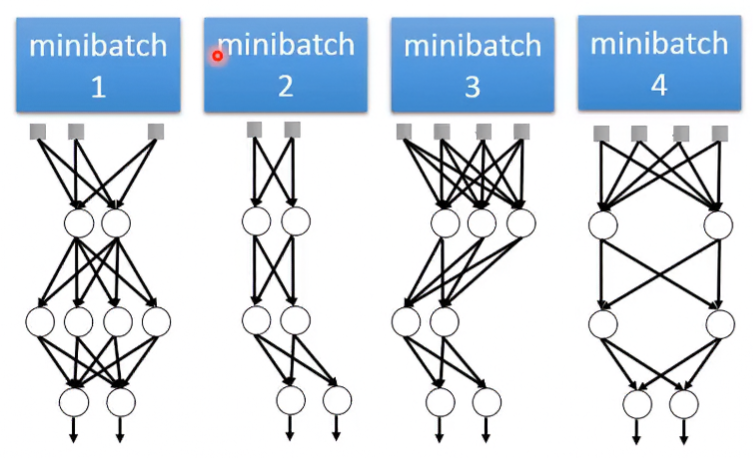
在Testing時，一樣無法把這麼多可能性的network都測試一遍，所以Dropout最厲害的地方在於，它可以對每個weight都乘上 1-p ，使得模型輸出可以近似於將所有可能性網路測試後平均起來的結果。